Lorsqu’il s’agit de communiquer des chiffres, qu’ils soient financiers, électoraux, démographiques, sportifs, scientifiques ou bien d’autres choses encore, tout le monde s’accordera pour dire qu’il n’y a rien de mieux qu’un graphique. Il est aujourd’hui difficile de trouver un journal qui ne contienne pas au moins une infographie ou un rapport d’activité quelconque qui ne soit pas truffé d’histogrammes et autres graphiques en “tarte” (pie chart en anglais). Et bien que la plupart des graphiques choisis soient particulièrement élémentaires – on trouve rarement autre chose qu’un graphique en ligne, un histogramme ou un graphique en tarte -, ils sont souvent mal utilisés. On voit souvent un graphique en ligne là où on aurait du voir un histogramme, certes, mais ça n’est pas le sujet de cet article. Très souvent, la réalité est tronquée, par malhonnêteté ou par ignorance, induisant une perception exagérée de ce que l’auteur veut mettre en avant. Voici quelques exemples glanés au fil de nos recherches, illustrant comment l’on essaye chaque jour de nous tromper.

Lie factor

De façon à pouvoir mesurer de façon formelle à quel point un graphique est une distorsion de la réalité (ou en tout cas des valeurs numériques que le graphique tente d’illustrer), Edward Tufte, auteur majeur dans le domaine de la visualisation de l’information (“The Visual Display of Quantative Information“), a défini le concept de “lie factor” (que l’on pourrait traduire par facteur de mensonge) de la façon suivante :

$$\text{lie factor} = \frac{\text{taille de l’effet dans le graphique}}{\text{taille de l’effet dans les donnees}}$$

où

$$\text{taille de l’effet} = \frac{| \text{seconde valeur} – \text{premiere valeur}|}{\text{premiere valeur}}$$

Un “lie factor” de 1 indique donc qu’il n’y a pas de distorsion. Tufte estime que ce facteur doit rester entre 0.95 et 1.05 pour assurer l’intégrité de la visualisation.¹

Par exemple, supposons que l’on veut indiquer dans un diagramme en bâtons (bar chart) qu’un produit A a été deux fois plus vendu qu’un produit B, il faut que la barre représentant A soit deux fois plus longue que celle représentant B. Cela peut paraître naturel… nous verrons dans les exemples qui suivent que c’est loin d’être toujours le cas !

Tronquer l’axe des ordonnées

Un des exemples de distorsion les plus fréquents est l’utilisation de diagramme en bâtons (bar chart) ou en ligne (line chart), représentant en ordonnée des quantités, et démarrant l’axe à une autre valeur que zéro.
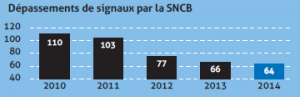Prenons par exemple l’illustration ci-contre, issue d’une infographie de la SNCB, parue dans le journal Métro du mercredi 10 juin 2015. On y montre la baisse du nombre de dépassements de signaux entre 2010 et 2014. Ils sont passés de 110 à 64, soit une baisse de 41.8 % ((110-64)/110). Par contre, visuellement, grâce au/à cause du fait que l’axe vertical démarre à 40 et non en zéro, la baisse est de 70 (110-40) à 24, soit 65.7 %. Notre cerveau enregistre une baisse drastique de quasiment un facteur 3. On a donc un lie factor de 65.7/41.8, soit 1.54. L’effet visuel est dès lors 54% plus important que les données à représenter ². 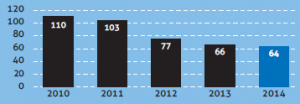Une version “corrigée” du graphique vous est présentée ci-contre. La diminution semble nettement moins impressionnante !

En cliquant sur l’illustration ci-dessus, vous apercevrez dans la même infographie trois diagrammes utilisant le même stratagème pour vanter la société, dont un avec un lie factor de 20.6 !

L’exemple suivant a été emprunté au parti socialiste français. 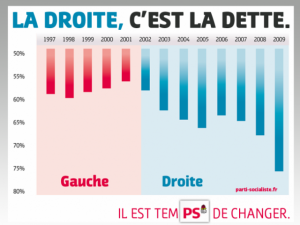Il met en avant une épouvantable évolution de la dette lorsque la droite s’est trouvée au pouvoir entre 2002 et 2009. Première chose intéressante à constater : alors qu’en général on représente la base d’un diagramme en bâtons en bas, les “communicants” du PS ont choisi ici de l’inverser. On observe donc une “montée” (quelque chose d’intuitivement positif) pour la gauche, et une “baisse” pour la droite (intuitivement négative).

Mais ce qui est plus important est de remarquer que l’axe vertical débute à 50 %. Alors que visuellement la dette semble avoir enregistré une progression de 317% entre la fin de la dernière valeur associée à la gauche et la dernière de la droite, elle n’a en fait crû que de +/- 57 % à 75 %, soit une progression de 33.9% (18% = 33.9% de 57%), et donc un lie factor de 317/33.9 = 9.3. On a donc une progression visuelle plus de neuf fois plus importante que la réalité ! Ce facteur serait plus bas si l’on considérait plutôt les valeurs moyennes de partie gauche et droite (au lieu, comme nous l’avons fait, du minimum pour l’un et du maximum pour l’autre), mais il en restera largement supérieur à 1.

Notons que cette règle, unanimement reconnue par la communauté scientifique s’intéressant à la visualisation de l’information et voulant que l’axe vertical d’un graphique doit toujours commencer à zéro, s’applique uniquement pour des valeurs pour lesquelles le zéro à une valeur intrinsèque, et signifie l’absence de quantité. Ce sont des valeurs pour lesquelles dire “deux fois plus grand” a un sens : 10 €, c’est bien deux fois plus que 5 €, 50 articles (identiques), c’est bien la moitié de 100 articles. Par ailleurs, cela ne dépend pas des unités utilisées : deux fois plus cher, c’est la même chose en euros ou en dollars, deux fois plus long, ça ne change rien que l’on s’exprime en mètres ou en pieds.

Il n’en ira pas de même lorsque la mesure que l’on considère a un zéro tout à fait arbitraire, comme ça l’est pour la température ou l’heure. On ne peut pas dire que quand il fait 20 °C, c’est deux fois plus chaud que 10 °C, ni que 10 heures du matin, c’est deux fois plus tard que 5 heures (on parle ici bien d’heure, et pas de durée). Minuit, ou 0 °C, ça n’est en rien l’absence d’heure ou de température ; ces valeurs sont choisies de façon conventionnelle. Minuit à Bruxelles ne correspond pas à minuit à New-York et 0 °C n’est pas la même température que 0 °F ou 0 °K. Étant donné qu’un graphique représentant une température au cours du temps ne représentera jamais un ratio ou une variation relative (qui ne serait par ailleurs pas la même si l’on s’exprimait en degrés Centigrades ou Fahrenheit) mais bien une variation absolue, l’origine de l’axe n’a pas d’importance. On évitera alors l’utilisation de diagrammes en bâtons (mettant en avant des longueurs) pour préférer une graphique en ligne (mettant en avant des positions).

Confondre surface et taille

Visuellement parlant, notre cerveau considère qu’un cercle (ou tout autre forme) est deux fois plus grand qu’un autre si sa surface est deux fois supérieure (et non son diamètre). Or on voit souvent des infographies dans lesquelles les diamètres sont proportionnels aux valeurs à représenter. Ce qui implique une relation quadratique entre ce que l’on voit et ce que l’on devrait voir : un ratio de 3 impliquera une surface 9 fois plus importante. Par ailleurs, il a été montré que le cerveau humain (entre autre par Jacques Bertin, dans son ouvrage “Sémiologie Graphique“, ou par Stanley Smith Stevens, dans sa “Psychophysical Power Law“) distingue moins précisément une différence entre deux surfaces qu’entre deux longueurs.

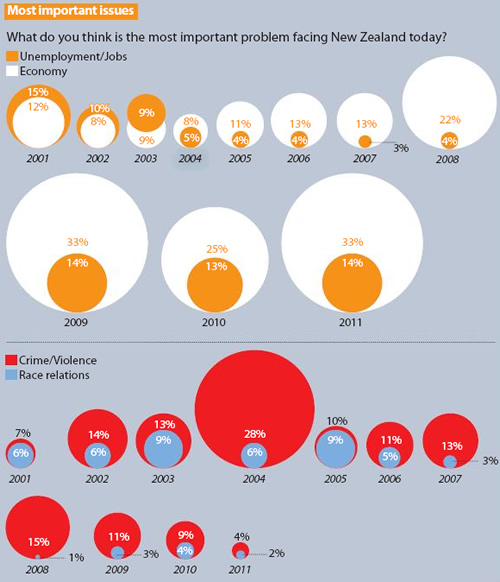Lorsque l’on mélange ces deux sources de confusions, on arrive à une infographie telle que celle présentée dans le “Sunday Star Times” du 12 février 2012 (reprise sur www.statschart.org.nz). Outre le fait qu’il existe des façons plus adaptées de représenter l’évolution de deux mesures dans le temps, on voit par exemple que le petit cercle orange de 2009 (14 %) a une surface 5.5 plus petite que le cercle dans lequel il est inscrit (33 %), soit une augmentation de surface de 450%, pour représenter en réalité une augmentation de 135% (14% -> 33%). Cela nous donne donc un lie factor de 3.32. Étant la relation quadratique entre diamètre et surface d’un cercle, le lie factor sera en fait différent pour chacun des graphiques (et d’autant plus important que le ratio dans les données est important). Le fait qu’un cercle soit placé devant l’autre est également trompeur : dans le premier item de la seconde infographie, la partie rouge est à peine visible, alors qu’elle représente une quantité supérieure à la partie bleue.

Jouer avec les perspectives

Un outil comme Excel vous permet – pour ne pas dire vous y incite – de rajouter des effets de perspective à vos graphiques. Si le résultat peut être visuellement élégant, il sera bon de s’en servir avec parcimonie, car il est particulièrement trompeur. 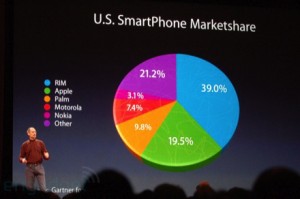Prenons l’exemple d’un graphique en tarte : non seulement les segments qui apparaîtront du côté du lecteur seront augmentés d’une “tranche” que n’auront pas les segments opposés, mais par ailleurs la perspective diminuera la surface les segments les plus éloignés. Dans l’exemple ci-contre, on peut voir Steve Jobs, en pleine “Keynote”, présentant la répartition du marché des principaux vendeurs de smartphones. Apple (19.5 %), en vert, occupe une surface à l’écran 1.8 fois supérieure à celle occupée par le segment “Autres” (21.2 %), en violet ! 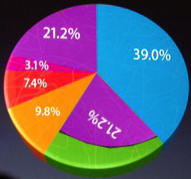On a donc, pour la comparaison entre ces deux éléments, un lie factor proche de 10 ! Pour mieux visualiser la “tromperie”, voici ci-contre une version du graphique dans lequel on superpose le segment violet des 21.2 % à celui, vert, des 19.5 %. En théorie, le vert devrait donc avoir complètement disparu. Jugez-en par vous-même…

Ignorer les conventions

Les graphiques standards se basent en général sur certaines conventions tacites, en principe naturelles. Par exemple, la somme des segments d’un graphique en tarte doit atteindre 100 %. 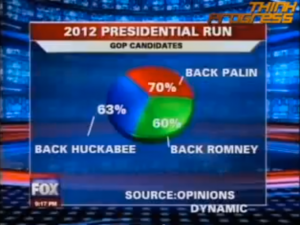Ce n’est pas exactement ce qu’a choisi de faire la chaîne américaine Fox pour diffuser ce graphique au moment des présidentielles américaines de 2012. Outre le fait que, dû à l’effet de perspective détaillé ci-dessus, le segment de Romney (60 %) est largement plus grand que celui de Palin (70 %), engendrant un lie factor de 3.7, la somme des segments monte à 193 % !  Il est probable qu’en l’occurrence, les sondés pouvaient donner deux choix, mais il faut reconnaître que ce graphique peut laisser perplexe !

Utiliser des valeurs cumulatives

Une excellente façon de masquer une baisse des ventes ou des revenus est d’utiliser des valeurs cumulatives. Elles ont l’avantage d’être, par définition, toujours croissantes. C’est par exemple ce qu’a choisi de faire Tim Cook lors de la Keynote de présentation de l’iPhone 5S. Il est en effet difficile de voir si, par exemple, la pente (c’est-à-dire le nombre d’unités vendues par quadrimestre) est plus forte début 2011 ou fin 2013 avec le graphique présenté ci-contre (sans compter sur le fait qu’on semble avoir “oublié” de préciser l’échelle de l’axe vertical). Sur la seconde image, David Yanofsky a réintroduit dans le graphique les données non cumulées. 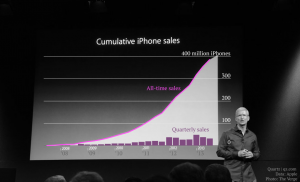Et là, surprise : alors que le graphique de Tim Cook suggère une augmentation explosive et continue, on s’aperçoit que les résultats ont plutôt tendance à se tasser.

Tromper les intuitions

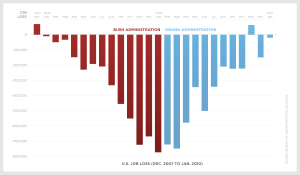Lorsque l’on voit un diagramme, on pense en général intuitivement qu’il représente une quantité (en fonction du temps, d’une catégorie…). Mais il peut aussi représenter une variation. C’est cette source de confusion qui a été utilisée par l’équipe d’Obama lors de sa seconde campagne en 2010, où on représente les “job loss” sous Bush (en rouge) puis sous Obama (en bleu). On a donc affaire à un problème exactement inverse à celui présenté juste ci-dessus.

On peut d’abord remarquer trois stratagèmes simples utilisés dans ce graphique pour accentuer le point de vue de l’auteur. Le premier a déjà été présenté avec l’exemple du parti socialiste français ci-dessus, et consiste à “retourner” le diagramme en bâton. On a donc quelque chose en décroissance sous l’administration Bush, qui accentue l’aspect dramatique, et en croissance sous celle d’Obama, pour accentuer le sentiment de progrès et de rétablissement. Par ailleurs, on voit un bleu clair, lumineux, pour la partie d’Obama et un rouge foncé, sombre pour celle de Bush. Ce n’est certainement pas innocent. Enfin, la légende indique le graphique va de 2007 à 2010. Si l’on ne fait pas attention aux mois, on pourrait penser que le graphique couvre 3, voire 4 ans, et qu’il s’agit donc d’une progression durable. Or le graphique concerne essentiellement 2008 et 2009 (décembre 2007-janvier 2010), soit à peine plus de deux ans.

Si l’on regarde ce graphique, qui concerne l’emploi aux États-Unis, on a l’impression d’une situation qui s’est terriblement détériorée durant le mandat de Bush, et qu’Obama est parvenu à rétablir. 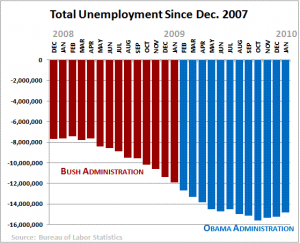Or le graphique ne représente pas le nombre de sans-emplois, mais bien le nombre de pertes d’emploi par semestre, soit la variation du nombre de sans-emplois. En regardant donc le graphique de plus près, on voit donc que le nombre de sans-emplois augmente moins vite, certes, mais ne diminue pas ou peu. Ce qui est en soi déjà un résultat important, mais qui est largement accentué avec ce graphique.

Le graphique ci-contre, généré par Soquel by de Creek, montre cette fois-ci le nombre total de sans-emplois (c’est-à-dire avec les valeurs cumulées). Il est nettement moins vendeur auprès des électeurs …

Mais encore…

Il existe de nombreuses autres façons de tromper le lecteur. Voici quelques exemples :

• Ignorer l’inflation quand on compare des budgets sur longues périodes. Comparer le budget Défense de Kennedy et d’Obama n’a par exemple pas de sens si l’on ne tient pas compte de la différence de la valeur du dollar entre les deux époques.
• Présenter des histogrammes dont les “bases” ne sont pas homogènes. Si l’on présente le total des ventes de chaque année mais que la dernière année représentée est toujours en cours, il faut ajuster les données pour ne pas donner l’impression d’une brusque baisse.
• Pour réaliser un effet de perspective, ne pas aligner la base des barres d’un histogramme, rendant très difficile la comparaison (exemple).
• Utiliser une échelle logarithmique lorsque ça ne se justifie pas, pour réduire visuellement l’écart entre deux valeurs.

Avoir ces quelques éléments en tête pourra être très utile, à la fois comme “consommateur”, pour éviter d’être leurré par une visualisation un peu trop vendeuse, mais également comme “producteur”, de façon à réaliser des graphiques les plus intègres possibles.

De très nombreuses illustrations de visualisations trompeuses ou mal conçues sont données sur le site wtfviz.net. Le manque de bon sens de certains est parfois surprenant…

---

Notes

1. Notons que la définition de Tufte peut prêter à confusion et est parfois contestée. En effet, lorsque l’on compare deux valeurs, on peut choisir arbitrairement quelle est la première et quelle est la seconde. Le choix impactera potentiellement fortement le calcul.
   Par ailleurs, si une augmentation de 10 % dans les données est traduite par une diminution visuelle de 5%, cela engendrera le même lie factor que si elle est traduite par une augmentation de 5%, étant donné l’utilisation de la valeur absolue.
   Certains préféreront une autre définition dans laquelle l’effet est calculé en effectuant le ratio entre les deux valeurs (première valeur/seconde valeur). Le choix des valeurs n’aura alors plus d’impact sur le lie factor, le choix étant bien entendu le même pour les données et pour le graphique.
2. Si on avait, comme précisé dans la note ci-dessus, inversé les première et seconde valeurs, on aurait eu un effet dans le graphique de 191.7 % ((70-24)/24), pour un effet dans les données de 71.9%, soit un lie factor de 2.66

Le titre de cet article est librement inspiré de nombreuses publications reprenant un nom très proche : How to lie with maps (Mark Monmonier, 1991), How to lie with statistics (Darrel Huff, 1954), How to lie with charts (Gerald Everett Jones, 2006)…