Obtenir un crédit auprès d’une banque est parfois un parcours du combattant. Une banque accepte à certaines conditions, une autre rejette la demande, une troisième encore consent à des conditions différentes de la première. Deux personnes ayant le même salaire, les mêmes avoirs en épargne et demandant le même montant peuvent obtenir des réponses différentes.

Avertissement : la suite est un exemple pédagogique visant à illustrer le principe du “machine learning”. Il ne se veut pas exact par rapport au fonctionnement du monde bancaire.

Une méthode qui pourrait aider la banque à faire son choix serait, à l’aide d’experts du crédit, de développer un “arbre de décision” : si le requérant a un salaire en CDI de plus de x% du remboursement mensuel, compter le nombre de défaut de payement des autres crédits. Si ce montant est inférieur à Y, accorder le crédit. Sinon, si le montant moyen de ses comptes d’épargne est supérieur à Z, accorder également, etc.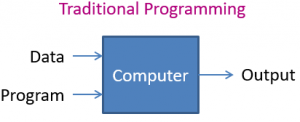

Définir un tel arbre peut être complexe, et parfois arbitraire, mais relèverait de la “programmation (informatique) traditionnelle” : on fournit à un ordinateur un programme (l’arbre de décision avec toutes ses branches, ses conditions et ses seuils) et des données (le montant du crédit demandé, le salaire, les avoirs, le montant des autres crédits en cours…), et il fournira un “output” (accorder ou non le crédit).

 

Programmation traditionnelle vs Machine Learning

Une approche plus puissante est d’utiliser l’apprentissage machine, ou “machine learning”. Le principe de base consiste à fournir à l’ordinateur un grand nombre de données sur le passé (appelées observations), concernant les crédits déjà accordés par la banque, puis de lui fournir le résultat (ou un “label”), à savoir le fait que le client ait pu ou non rembourser son crédit (on pourrait être plus fin en définissant des catégories : “a remboursé son crédit sans difficulté”, “a eu entre A et B retards de payements”, …, “a été en défaut de payement”). Sur base de ceci, le machine learning consiste à entraîner l’ordinateur pour qu’il soit capable de produire un programme qui pourra, sur base des données d’une future demande, prédire si oui ou non le client remboursera ses dettes.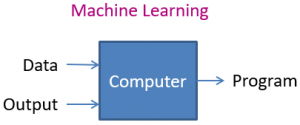

Les données en question, on peut les voir comme un grand tableau, avec une ligne par crédit accordé par le passé (observation), et une colonne pour chaque donnée, que l’on appelle “feature” ou “variable”: le montant du crédit, le salaire, le montant des autres crédits, le nombre de retard de payements… et peut-être aussi des features moins avouables (le genre du/de la client(e), ou le montant des dépenses en pharmacies dans les 6 derniers mois…). On peut très bien ajouter des features sans savoir si elles auront un quelconque impact sur le résultat, et laisser l’ordinateur le découvrir. 

Pour être plus précis, l’ordinateur ne va pas créer un programme “à partir de rien”: on va en fait choisir un algorithme de machine learning (Decision Tree, Random Forest, Gradiant Boosting…) et l’entrainement permettra de choisir les paramètres de l’algorithme (qui peuvent être plusieurs milliers, voire plusieurs millions dans le cas de la “deep learning”, une des familles les plus récentes des algorithmes de machine learning). Cet algorithme “paramétré” pourra ensuite être utilisé en production lorsqu’une nouvelle demande de crédit sera soumise à la banque.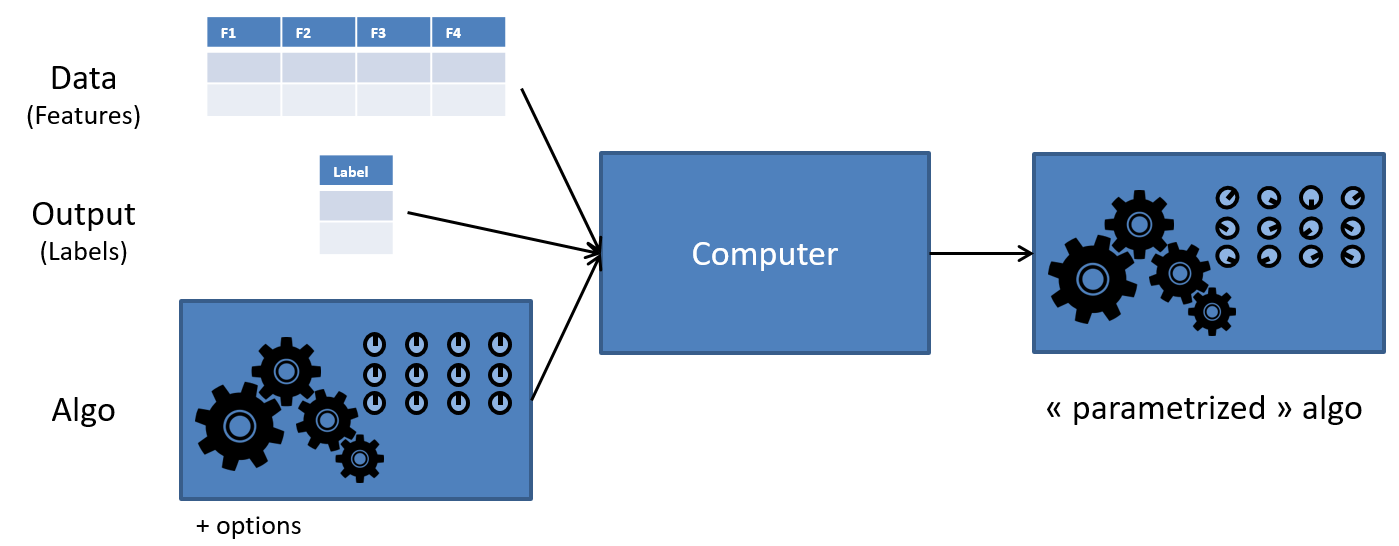

 

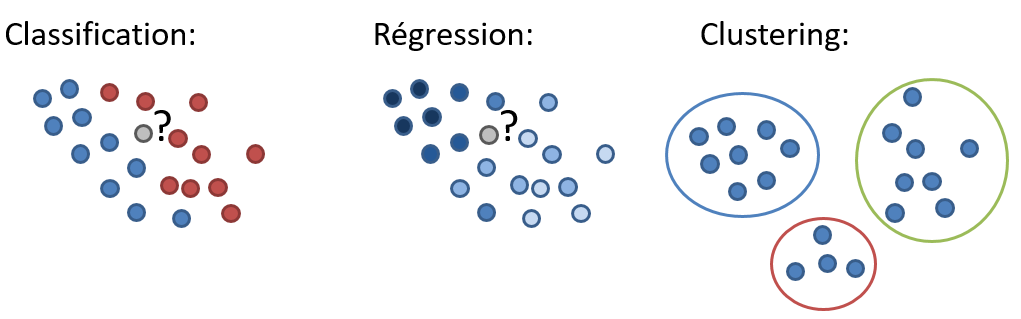
Classification, regression, clustering

L’exemple que nous avons donné ci-dessus illustre les algorithmes de “classification” : à partir des données d’entrée (features) associées à des labels connus, on entraîne le modèle à déterminer une catégorie, ou une classe, pour un nouvel arrivant : “accorder le crédit”, “refuser le crédit”. Il est aussi possible d’utiliser un algorithme de régression: à partir des features et des labels, déterminer une valeur numérique (montant à accepter, taux du crédit…). Ces deux groupes (classifications et régression) font partie de la famille des méthodes supervisées, parce qu’un résultat attendu (le label) est fourni pour les données d’entrainement. 

Il existe aussi une famille de méthodes non-supervisées, lorsqu’on ne fournit pas de label. On parle principalement de “clustering“, le but étant d’arriver à déterminer automatique des groupes de clients (dans notre cas) ayant des caractéristiques similaires.

Avec des graphes ?

Dans ce blog (voir par exemple ici ou ici), nous avons souvent montré la puissance de l’analyse réseau, qui consiste à ne plus considérer les données comme des individus ayant chacun un certain nombre de caractéristiques, mais comme des entités liées entre elles par des relations. Dans notre cas, on pourrait considérer un modèle simple avec des comptes bancaires et des personnes, les relations entre comptes bancaires représentant les transactions, et celles entre personnes et comptes, l’appartenance. On peut facilement ensuite enrichir le modèle avec les domiciles des personnes et les numéros de téléphones, comme illustré ci-dessous.

Cette (nouvelle) façon de voir le problème permet de donner des perspectives supplémentaires à notre analyse. Voici quelques méthodes permettant d’augmenter les performances de notre moteur de décision. 

Pattern based features

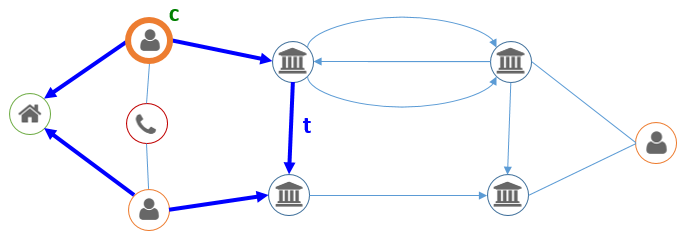
En analyse réseau, on identifie souvent des “patterns“, ou des schémas, qui sont pertinents, spécifiquement pour le business étudié. On pourrait par exemple imaginer qu’une transaction entre deux personnes domiciliées à la même adresse ne doit pas être considérée de la même façon qu’entre deux personnes non-apparentées. On pourrait dès lors exclure ces montants – qui peuvent être vus comme des mouvements d’équilibrage internes entre les membres d’un même foyer – des dépenses totales du client. Dans un langage comme “Cypher” (le langage de requêtage de la base de données graph Neo4j), une telle transaction “t” pour un client “c” serait identifiée comme telle: 

(c:Client)-[:OWNS]->(:BankAccount)-[t:TRANSFERS]->(:BankAccount)<-[:OWNS]-(:Client)-[:LIVES_AT]->(:Address)<-[:LIVES_AT]-(c)

Dans cet exemple, “(c:Client)” désigne un nœud de type “Client”, nommé “c”, identique au dernier nœud du pattern ; et -[:OWNS]-> désigne l’appartenance d’un compte à une personne.

Cette description correspond au chemin ci-dessous : 

Dans le secteur de la lutte contre la fraude, on pourrait être intéressé par les personnes ayant effectué des virements vers des personnes ayant été convaincues de fraude par le passé, voire vers personnes vivant à la même adresse que des personnes négativement connues : 

• (c:Client)-[:OWNS]->(:BankAccount)-[:TRANSFERS]->(:BankAccount)<-[:OWNS]-(:Client {isFraudster:True})
• (c:Client)-[:OWNS]->(:BankAccount)-[:TRANSFERS]->(:BankAccount)<-[:OWNS]-(:Client)-[:LIVES_AT]->(:Address)<-[:LIVES_AT]-(:Client {isFraudster:True})

Où (:Client {isFraudster:True}) désigne un nœud de type “Client” ayant un attribut “isFraudster” de valeur “True”.

Sur base de ces patterns, on peut ajouter des nouvelles features aux données décrites plus haut dans cet article, soit booléennes (existe-t-il pour ce client des transactions vers des clients “fraudeurs”), soit numérique (fréquence des “auto-transferts”, ou ratio entre ceux-ci et les autres). Il n’est de nouveau pas nécessaire d’être sûr que la valeur soit corrélée avec le risque de défaut de payement : on laissera aux algorithmes de machine learning le soin de découvrir si elle est pertinente ou non.

Graph based features

L’avantage des méthodes décrites dans la section précédente est qu’elles permettent de rajouter des features qui sont très pertinentes et spécifiquement sélectionnées pour le domaine en question. La contrepartie est qu’elles peuvent être difficiles à identifier et à implémenter. Il existe cependant de nombreux algorithmes génériques pour les graphes, qui peuvent s’appliquer à très faibles coût, tout en proposant des métriques pertinentes. En particulier, les différentes méthodes de calcul de centralité (degree centrality, betweenness centrality, closeness centrality, PageRank…) donnent à chaque nœud (ou à chaque nœud d’un type spécifique) une valeur numérique qui peut être utilisée comme feature.

D’un autre côté, les méthodes de détection de communauté (Louvain, Label Propagation…) attribuent une catégorie (ou une communauté) à chaque nœud.  On peut l’utiliser directement, si l’algorithme de machine learning supporte les features catégoriques, ou indirectement, en comptant par exemple le ratio entre les transferts entre comptes appartenant à la même communauté et ceux des communautés distinctes.

Les algorithmes plus courts chemins peuvent également être pertinents : on peut par exemple considérer la distance du client à un client fraudeur, ou en défaut chronique de payement, si l’on part du postulat, certes moralement discutable, qu’une personne a plus de chances d’être en défaut de payement si elle est entourées de nombreuses personnes chroniquement en défaut de payement.

Notons que ces méthodes se servent en général uniquement de la topologie du réseau, et pas des attributs (ou éventuellement d’uniquement un attribut désignant un “poids” ou une distance). Toute la connaissance n’est donc pas utilisée.

Graph embeddings

En dehors des méthodes qui peuvent fournir des métriques dont la sémantique est en générale claire (un nœud avec un grand “PageRank” sera considéré comme “plus important” qu’un nœud en ayant un petit), il existe une série des méthodes (fastRP, node2Vec, GraphSAGE) qui permettent de calculer pour chaque nœud un nombre déterminé de valeurs (on parle de vecteur), qui offrent une sorte de résumé de la position du nœud au sein du graphe. Il s’agit du même principe que pour le “word embedding” en NLP.

Si l’on choisit de calculer un graph embedding de taille 16, on obtiendra donc 16 features utilisables par les algorithmes traditionnels de machine learning. Aucune de ces nouvelles colonnes ne sera interprétable en tant que tel. L’ensemble n’aura pas non plus de sémantique humainement compréhensible, mais on observe qu’elle peuvent néanmoins être pertinentes pour un algorithme de machine learning. On peut donc voir le “graph embedding” comme une sorte de fonction de hashing pour chaque nœud, dont la valeur n’est pas interprétable par un être humain, mais l’est par un ordinateur (plus précisément un algorithme de machine learning).

Graph native learning

Les méthodes présentées ci-dessus consistent à “faire rentrer un rond dans un carré”: on fait en sorte de faire rentrer dans un modèle tabulaire des données graphes qui ne le sont fondamentalement pas. Ceci permet de profiter de l’arsenal extrêmement bien développé et mature qu’est le machine learning, au détriment de la richesse du modèle graphe. 

Mais il existe depuis peu (dans Neo4J, depuis les premières versions de la librairie GDS, en 2020 ; mais la littérature est bien plus ancienne) des méthodes de machine learning spécifiquement dédiées aux graphes, qui ne nécessitent pas cette transformation tabulaire. 

La principale méthode est celle de la prédiction de lien (link prediction) : elle consiste à estimer si des relations ne sont pas manquantes dans le graphe. Par exemple, dans un graphe qui établit des interactions connues entre des molécules (médicaments, polluants…), on pourra suggérer d’étudier des interactions non-identifiées. Idem pour des interactions entre des clients et des produits (achetés, aimés, consultés…), qui permettra de faire des recommandations pertinentes aux clients.

Conclusions

Dans un rapport récent, Gartner estime que d’ici 2025, les technologies de graphe seront utilisées dans 80% des innovations en analytique, pour seulement 10% en 2021. Il y a donc un énorme potentiel de progression pour les technologies de graphe, et il est clair que le machine learning occupera une place considérable dans cette (r)évolution. Mais il ne sert à rien de mettre la charrue avant les bœufs : une transition vers le “Graph Machine Learning” ne peut pas être réussie si l’on ne maîtrise ni les technologies graphes (et les bases de données orientées graphe) ni le machine learning. Et pour beaucoup d’entreprises ou d’administrations, il reste un travail considérable pour prendre ce train en marche. Mais il n’est pas trop tard!

---

Ce post est une contribution individuelle de Vandy Berten, spécialisé en data science chez Smals Research. Cet article est écrit en son nom propre et n’impacte en rien le point de vue de Smals.