Dans notre article précédent, nous avons montré que beaucoup d’information pouvait être trouvée rien qu’en parcourant la liste d’amis Facebook de quelqu’un, et en analysant les relations d’amitié entre ceux-ci. Il semble donc raisonnable de penser qu’il est prudent de rendre sa liste d’amis privée, ou à tout le moins uniquement accessible à ses propres amis. Ceci peut se faire en cliquant le petit crayon en haut à droite de sa propre liste d’amis (https://www.facebook.com/me/friends). Malheureusement, nous allons voir dans cet article que, même avec cette option activée, il est facile de reconstituer une partie non négligeable du réseau d’une personne. Nous verrons deux astuces pour y arriver. La première réside dans le fait que si A est ami avec B, et que A cache sa liste d’amis mais pas B, on ne peut pas voir qu’ils sont amis sur le profil de A, mais on pourra le voir sur le profil de B. La seconde se base sur les suggestions d’ajout que Facebook propose.

Nous insistons sur le fait que le but de cet article n’est pas de donner des outils à des gens mal intentionnés (les techniques présentées ici sont largement connues de la communauté des hackers), mais d’attirer l’attention du citoyen lambda sur ce qui peut être fait à partir des informations qu’il dissémine sur les réseaux sociaux.

Via les amis mutuels

En mai dernier, le chercheur en sécurité Shay Priel faisait remarquer ce qui lui semblait être une vulnérabilité de Facebook (et que Facebook considère comme une fonctionnalité) permettant de reconstituer la liste d’amis de n’importe quel profil. Supposons que l’on s’intéresse à une cible T, qui cache sa liste d’amis.  Si je me rends sur https://www.facebook.com/T/friends (remplacer “T” par un nom d’utilisateur Facebook pour obtenir un véritable exemple), une liste vide s’affichera.

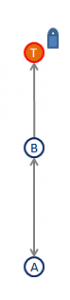
Supposons maintenant que je sois parvenu à déterminer qu’un certain A est ami avec T, et que ce A ne cache pas sa liste d’amis. Si je me rends sur sa liste d’amis (https://www.facebook.com/A/friends), je pourrai y trouver T, ce qui m’indiquera que T est un ami de A. Étant donné que la relation d’amitié sur Facebook est symétrique, je sais également que A est un ami de T.

Relâchons maintenant ma contrainte, et supposons que A n’est pas forcément amis avec T, mais qu’ils aient uniquement des amis en commun. Si je rajoute à l’adresse ci-dessus “?and=T” (soit, donc  https://www.facebook.com/A/friends?and=T), et que A accepte toujours de publier sa liste d’amis, j’obtiendrai une liste de profils qui sont des amis mutuels de T et A (B dans le schéma ci-contre), et donc, par définition, de T également. Notons que seuls apparaîtront dans cette liste ceux qui ont gardé publique leur liste d’amis.

Si j’ai bien choisi A, je viens donc d’obtenir quelques amis de T. Il me suffit maintenant, pour chaque ami B de A, de refaire la même chose que pour A (https://www.facebook.com/T/friends?and=B). J’obtiendrai probablement en partie les mêmes amis, mais, avec un petit peu de chance, également l’un ou l’autre nouveau (en plus de A que j’obtiendrai nécessairement). Pour autant que je puisse trouver quelques candidats de départ, je pourrai ainsi, de proche en proche, construire une partie du réseau de ma “cible”. Nous verrons plus bas que nous avons, de cette façon, retrouvé 80% des amis ayant leur liste d’amis publique du profil de l’auteur de cet article.

Notons qu’avec le processus ci-dessus, on trouve non seulement les nœuds de mon graphe (voir l’article précédent pour plus de détails), mais également les connexions : je peux établir une connexion entre B et tous les profils repris sur la page https://www.facebook.com/T/friends?and=B.

Le processus décrit ci-dessus peut être très laborieux. Nous attirons cependant l’attention sur le fait que l’utilisation de script permettant une automatisation de cette construction, comme celui proposé par Shay Priel, est contraire aux conditions d’utilisation de Facebook (point 3.2), et l’auteur s’expose donc à une suspension de son compte Facebook sans préavis.

Initialisation du processus

Pour initier ce processus, il faut trouver l’un ou l’autre profil ayant des amis communs avec T (mais pas forcément étant ami avec T). Une façon simple est de se servir de l’outil “Graph Search”, présenté dans un article précédent. Une requête telle que “People tagged in photos of T” liste toutes les personnes taguées dans des photos publiques sur lesquelles T est également tagué. Il y a donc des chances qu’il y ait l’un ou l’autre ami (d’amis) de T parmi celles-ci.

On peut également se baser sur l’appartenance à des groupes, et choisir comme requête “People of groups T joined“, ou “People who like [une page que T pourrait aimer]“. Il est également possible de se baser sur le nom de famille (Find all people named “[Nom de famille de la cible]”), dans l’espoir de tomber sur l’un ou l’autre cousin, père ou autre sœur (ce qui peut être une approche très longue s’il s’agit d’un nom de famille répandu). De multiples possibilités sont disponibles, y compris celles d’avoir déjà suffisamment d’information sur la cible pour en connaître quelques amis.

Notons qu’avec cette technique, dont l’efficacité est illustrée plus bas, rien ne permet à la cible de se rendre compte que quelqu’un tente de reconstituer son réseau.

Nous avons appliqué la technique présentée ci-dessus (en partant des personnes taguées) sur le profil de l’auteur de cet article, dont la liste d’amis est cachée. La liste réelle comprend 561 nœuds (voir l’article précédent pour plus de détails), et, parmi ceux-ci, 300 seulement ont rendu leur liste d’amis publique. Nous avons retrouvé grâce à cette méthode 249 amis, soit 44% du total (561), mais 83% des amis avec une liste d’amis publique (300), qui sont les seuls qu’il est possible de retrouver par cette méthode.

Via les suggestions de Facebook

Une seconde méthode, présentée par Irene Abezgauz se base sur les suggestions d’amis que Facebook fait en permanence pour aider les utilisateurs à étendre leur réseau. Elle consiste à créer un compte Facebook “bidon”, et à envoyer à partir de ce compte une demande d’amitié à la cible. Même si la cible ignore la requête ou la refuse, étant donné que le compte “attaquant” est vierge, le seul élément dont Facebook dispose pour suggérer des nouveaux amis est la liste d’amis de la cible. Et c’est bien ce qu’on observe… Il suffit de se rendre maintenant sur www.facebook.com/friends/requests/ pour voir apparaître une série de suggestions qui ne sont autre que des amis de la cible. Ils n’apparaissent cependant pas tous : toujours sur le compte de l’auteur de cet article, 89 suggestions ont été faites, toutes correctes. La même requête faite à d’autres moments donne exactement le même résultat, mais un essai avec un autre compte “bidon” donne d’autres résultats : 99 suggestions nous ont été faites avec cet autre compte, dont près de la moitié ne faisaient pas partie des suggestions du premier compte.

Par ailleurs, parmi ces quelque 150 amis listés, 35 n’avaient pas été trouvés par la méthode présentée dans la section précédente. Et en ré-appliquant l’algorithme de recherche d’amis mutuels sur ces nouveaux amis, nous avons obtenu au total 297 amis, soit 99% des 300 amis rendant leur liste d’amis publique ! Nous aurions probablement pu encore augmenter ce score en créant de nouveaux comptes “bidon”.

Notons que cette méthode est moins transparente que la précédente, puisque la cible reçoit une demande d’amitié, qui pourrait sembler suspecte.

Approximation de la structure

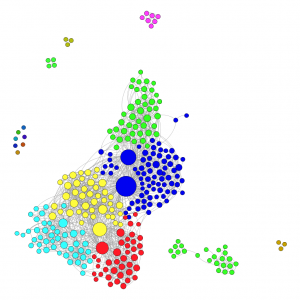
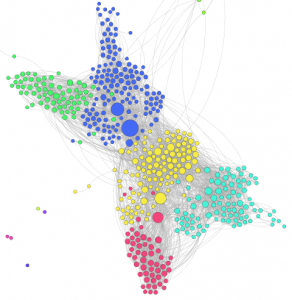
En appliquant l’analyse de modularité (voir article précédent) sur le graphe ainsi créé (voir figure ci-contre), nous avons pu constater que, en dehors des profils tout à fait isolés, 91% des profils ont été classés dans la même classe que lorsque nous avions la totalité du graphe. Par ailleurs, près de la moitié des différences provient de deux de mes cercles sociaux ayant beaucoup de connexions, avec un certain nombre de personnes faisant partie des deux.

Le tableau suivant reprend plus en détails l’exactitude des résultats. Les deux premières colonnes reprennent la proportion de nœuds par rapport au total ayant été classés dans le groupe de la ligne. La troisième colonne indique la proportion de nœuds du groupe de la ligne ayant été classés pour le graphe extrait avec la méthode ci-dessus dans le même groupe qu’avec le graphe complet.

	Graphe complet	Graphe extrait	% égaux
Groupe 1	25%	26%	91%
Groupe 2	16%	14%	88%
Groupe 3	13%	15%	91%
Groupe 4	13%	14%	100%
Groupe 5	12%	13%	85%
Groupe 6	12%	13%	100%

Deviner des amis

Nous avons essayé d’aller plus loin, en cherchant à savoir s’il était possible de trouver des amis qui rendent leur liste privée, à partir du moment où l’on acceptait un certain degré d’erreur dans le résultat (c’est-à-dire potentiellement considérer comme ami quelqu’un qui ne l’est pas). L’idée est la suivante : si un grand nombre d’amis de T disent être amis avec A, il est probable que A et T soient en réalité amis, même s’ils cachent tous les deux leur liste d’amis. Pour ce faire, nous avons listé la totalité des amis de chaque ami de T publiant sa liste d’amis, et avons étudié les recouvrements.

En fixant un seuil à 15 amis communs, nous avons obtenu 72 amis potentiels de votre serviteur. Parmi ces 72, 61 faisaient réellement partie de mes amis sur Facebook, mais rendaient, tout comme moi, leur liste d’amis privée; j’en connaissais personnellement 8 autres, et j’estime qu’ils me connaissent également (sans que nous ne soyons amis sur Facebook), et seuls 3 m’étaient très vaguement ou pas du tout connus. En considérant que quelqu’un s’intéresse à mon réseau social “réel” (c’est-à-dire les personnes que je connais, peu importe que nous soyons amis sur Facebook ou non), on aurait pu retrouver près de 370 de mes amis, avec seulement 3 “erreurs”.

En fixant par contre le seuil à 10, 173 auraient été trouvés, dont 120 effectifs sur Facebook (avec liste privée), 32 connus en vrai mais pas amis sur Facebook et 21 inconnus ou très vague. Le taux d’erreur devient alors plus élevé, et le problème est que seule la cible (moi, en l’occurrence) est capable de dire si l’approximation est correcte ou non, ce qui complique la tâche de l’attaquant. Une recherche plus approfondie, à partir d’un certains nombre de “cibles collaborantes”, prêtes à faire la même expérience, permettrait sans doute de déterminer un seuil raisonnable ou optimal, en fonction de paramètres à déterminer. Mais le travail, qui doit largement être mené à la main, est très laborieux.

Nous n’avons pas étudié de méthodes plus avancées, mais il serait probablement possible d’améliorer cette technique, par exemple en pondérant les amis communs en fonction de leur centralité : une personne ayant 10 amis communs avec une haute centralité de degré moyen (ou une autre définition de centralité) avec la cible a sans doute plus de chance d’être amie avec la cible qu’une personne ayant 10 amis en commun ayant tous une faible centralité de degré.

Conclusions

Comme nous le montrent cet article et les deux précédents (à propos des photos ou de la structure des réseaux), les réseaux sociaux, et Facebook en particulier, regorgent d’informations sur ceux y sont inscrits. Il n’est même pas nécessaire d’en être un utilisateur actif : je n’ai qu’une utilisation très passive de Facebook, et ne poste quasiment jamais rien, certainement pas publiquement.

L’utilisateur n’a que très peu de contrôle sur ces informations, car elle sont souvent implicites (émanant de la structure des connexions, ou de la fréquence d’apparition d’information) ou dans les mains d’autres utilisateurs (difficile de demander à chacun de ses amis de masquer sa liste d’amis, de cacher son appartenance à tel ou tel groupe ou de supprimer toutes ses photos).

Ceci n’est bien évidemment pas un appel au boycott : à chacun à faire la balance entre ce que les réseaux sociaux lui apportent en termes humain, de loisir ou autre, et l’information très précieuse que l’on donne à son propos, qui dépasse très largement celle qu’on fournit explicitement. Nous espérons que cette série d’articles permettra au lecteur de le faire de façon plus éclairée !