Grâce à leur capacité à comprendre et exploiter les relations complexes entre les données, les technologies relatives aux graphes ont actuellement le vent en poupe, gagnant en popularité dans de nombreux domaines de l’intelligence artificielle et la gestion de données. Plusieurs articles ont d’ailleurs déjà été postés sur ce blog concernant différentes technologies de graphes, notamment sur les bases de données orientées graphe (graph database) [1, 2, 3] et les graphes de connaissances (knowledge graph) [4, 5, 6].
Mais que recouvre réellement le terme « graphe » ? Entre les modèles mathématiques qui servent de fondation, les bases de données orientées graphe et les graphes de connaissances, il peut être difficile de s’y retrouver et d’identifier les outils adaptés à ses besoins. Ajoutez à cela le fait que travailler sur des données organisées en réseau peut sembler complexe à première vue et que l’utilisation d’algorithmes de graphe ne fait pas partie des compétences de base de la plupart des data engineers et data scientists, et tout cela peut rendre décourageant la création et l’exploitation de données et de modèles de graphes.
Cet article a donc pour objectif de faire le point sur les technologies graphes, en explorant les 3 aspects mentionnés ci-dessus :
- Les graphes d’un point de vue théorique, leurs propriétés, leurs applications principales ;
- Les bases de données orientées graphe, spécialisées dans le stockage et l’exploitation de données connectées ;
- Les graphes de connaissances qui structurent le savoir de manière sémantique.
Le but est donc de présenter ces concepts, les frontières – parfois floues – qui les séparent, ainsi que de mettre en lumière leurs utilisations et les outils et logiciels qui y sont associés.
Cet article est divisé en deux parties. Cette première partie est consacrée aux graphes dans leur forme mathématique fondamentale, comment les encoder et les exploiter, ainsi qu’aux principaux algorithmes et leurs applications. La seconde partie portera sur les bases de données orientées graphe et graphes de connaissances et les outils qui y sont associés.
Retour aux fondamentaux : les graphes en tant que structure mathématique
Avant toute chose, commençons par définir ce qu’est un graphe. Cette base théorique est cruciale car c’est dessus que se construisent les concepts de base de données orientée graphe et de graphe de connaissances. À tout moment, ces concepts plus avancés peuvent être ramenés à leur forme mathématique sous-jacente et, par extension, tous les modèles et algorithmes présentés ci-dessous sont applicables à des bases de données orientées graphe et graphes de connaissances.
Dans sa forme la plus fondamentale, un graphe est une structure mathématique constituée d’un ensemble de nœuds et d’arcs qui joignent des nœuds deux à deux. Les nœuds représentent typiquement des objets ou des personnes, et les arcs représentent des liens entre ces objets ou personnes. Par exemple, dans le cas d’un réseau social, un arc peut représenter un lien d’amitié entre deux utilisateurs.
Le graphe peut être soit dirigé soit non-dirigé. Dans le cas d’un graphe non-dirigé, les relations entre les nœuds sont toujours réciproques (par exemple, un lien d’amitié sur Facebook) alors que dans un graphe dirigé, un arc allant d’un nœud i à un nœud j n’implique pas forcément d’arc de sens opposé (par exemple, un site internet A ayant un hyperlien qui pointe vers un site B).
Suivant la situation ou l’application, un graphe peut aussi être pondéré ou non. Un graphe est dit pondéré lorsqu’un poids est associé à chaque arc, qui varie d’un arc à l’autre, et qui permet de donner plus de « force » à certains arcs. L’interprétation de ces poids dépend du contexte, ces poids peuvent par exemple représenter un degré d’affinité, de similarité, de dépendance, etc.
Un graphe est généralement représenté par une matrice carrée de dimension (n × n), où n est le nombre de nœuds du graphe, appelée matrice d’adjacence (notée A). L’élément en position (i, j) dans la matrice vaut le poids de l’arc allant du nœud i au nœud j s’il existe, et 0 sinon (voir Figure 1). La matrice d’adjacence est simplement une matrice binaire lorsque le graphe n’est pas pondéré.
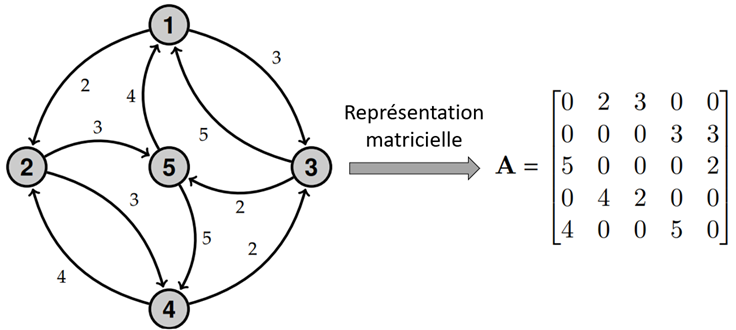
Dans l’exemple illustratif, il y a un arc de poids 3 allant du nœud 1 au nœud 3, et un arc de poids 5 allant dans le sens inverse. La matrice A contient donc la valeur 3 en position (1,3) et la valeur 5 en position (3,1).
Il est à noter que les matrices d’adjacence contiennent souvent une très large majorité de zéros, et sont donc généralement encodées via des matrices creuses (sparse matrix) afin d’optimiser la mémoire.
Cette représentation d’un graphe sous forme d’une matrice facilite fortement l’utilisation d’algorithmes sur le graphe, car nombre d’algorithmes de graphe, parfois complexes sous forme d’équations, peuvent souvent être résumés à une série d’opérations matricielles élémentaires. Ceci rend leur exécution très efficace dans des langages de programmation scientifiques optimisés pour les calculs matriciels, tels que R, MATLAB, Julia ou Python (numpy, scipy).
Utilisations d’algorithmes de graphe et applications pratiques
Pour mieux comprendre l’intérêt d’un graphe, commençons dans un premier temps par regarder les grandes catégories d’algorithmes de graphe, avec, pour chaque catégorie, quelques exemples d’utilisation pratique de ceux-ci.
- Déterminer le chemin optimal permettant de joindre une paire de nœuds.
Il peut simplement s’agir de minimiser le nombre de transitions nécessaires pour passer d’un nœud à l’autre, ou alors, si un coût est associé à chaque arc, de trouver le chemin associé au coût le plus faible. Le coût peut-être défini en tant que poids d’un arc, ou encodé dans une seconde matrice (matrice de coût, indépendante de la matrice d’adjacence). La façon dont le coût d’un arc est déterminé dépend de l’application, en fonction de ce que l’on souhaite minimiser. Il peut s’agir, par exemple, d’une mesure de longueur de l’arc (telle que la longueur d’une route), une mesure de temps (le temps nécessaire pour franchir l’arc) ou un coût financier. Ce genre d’algorithme peut être utilisé en logistique pour optimiser le transport. Les algorithmes les plus connus en la matière étant les algorithmes de Dijkstra, A*, ou encore l’algorithme de Bellman-Ford.
- Établir des mesures de similarité ou de distance entre des nœuds d’un graphe.
Suivant le contexte, il peut être intéressant d’établir une mesure de similarité entre deux nœuds d’un graphe afin de déterminer à quel point ils sont proches l’un de l’autre. L’utilisation de mesures de similarité est une approche souvent utilisée dans les applications de recommandation. En construisant un graphe de consommation qui lie les utilisateurs aux produits qu’ils ont consommés, mesurer la similarité entre les nœuds permet d’identifier, pour un utilisateur donné, des utilisateurs ayant un profil de consommation similaire, en se basant sur leurs liens avec les produits. Typiquement, un produit sera recommandé à un utilisateur soit parce qu’il a été consommé par de nombreux utilisateurs similaires (user-based recommendation) soit car le produit est similaire à ceux déjà consommés par l’utilisateur (item-based recommendation). Les mesures de similarité les plus connues se basent généralement sur des mesures de voisinage commun (le nombre de voisins en commun que possèdent deux nœuds), telles que l’indice de Jaccard ou la similarité cosinus, mais d’autres méthodes permettent de prendre aussi en compte le voisinage indirect, telles que le kernel de Katz [12] (aussi connu sous le nom de « von Neumann kernel »). Pour voir quelques mesures de similarité classiques et leur utilisation en recommandation, voir [13].
L’opposé d’une mesure de similarité est une mesure de dissimilarité, qui augmente à mesure que les deux nœuds sont différents. Une mesure de distance est, par définition, une dissimilarité, puisqu’elle augmente lorsque deux nœuds sont éloignés. La mesure de dissimilarité la plus connue et la plus intuitive entre deux nœuds est la longueur du plus court chemin qui les sépare.
- Mesurer la centralité.
Une mesure de centralité d’un nœud ou d’un arc, parfois aussi appelée mesure de prestige, sert à quantifier à quel point un nœud ou un arc est important au sein d’un graphe. La mesure de centralité la plus connue est, de loin, le score calculé par l’algorithme PageRank [14]. Initialement développé et utilisé par le moteur de recherche Google pour hiérarchiser les pages web, PageRank se base sur une marche aléatoire sur un graphe où chaque nœud représente une page web et chaque arc dirigé représente un hyperlien entre deux pages. L’algorithme PageRank trouve de nombreuses applications au-delà de la hiérarchisation de pages web :
“Google’s PageRank method was developed to evaluate the importance of web-pages via their link structure. The mathematics of PageRank, however, are entirely general and apply to any graph or network in any domain. Thus, PageRank is now regularly used in bibliometrics, social and information network analysis, and for link prediction and recommendation. It’s even used for systems analysis of road networks, as well as biology, chemistry, neuroscience, and physics.” – Gleich (2014) [15]
Un autre algorithme très connu, similaire à PageRank, est l’algorithme HITS (Hyperlink-Induced Topic Search) [16].
Lorsque l’on parle de centralité, PageRank est souvent l’algorithme présenté, cependant, la centralité peut se comprendre de plusieurs manières. Il peut par exemple s’agir d’un nœud ou d’un arc constituant un intermédiaire critique pour la communication et la transmission d’information au sein du réseau. Repérer des nœuds centraux peut par exemple permettre d’optimiser la diffusion d’information dans un réseau ou de détecter des nœuds ou des arcs vitaux au graphe (dont la disparition nuirait fortement à la transmission d’information dans le graphe). Des mesures fréquentes de centralité de nœuds ou d’arcs se basant sur ce principe utilisent généralement des mesures « d’intermédiarité » (betweenness centrality).
La centralité peut aussi se comprendre comme la mesure de la représentativité d’un nœud au sein d’une communauté (en termes de proximité vis-à-vis des autres nœuds du graphe), se mesurant ici plutôt avec une mesure de proximité (closeness centrality). Il est à noter que nous avons déjà mentionné l’utilisation de différents algorithmes de centralité dans un cadre de détection de fraude dans des articles de blog précédents, notamment PageRank (sous forme d’un algorithme de diffusion) [7] et la betweenness centrality [8].
- Partitionner le graphe.
Plus connu sous le nom de « clustering », le partitionnement de graphe consiste à regrouper des nœuds en communautés (clusters) tels que les nœuds au sein d’une communauté sont « similaires » et deux nœuds appartenant à des communautés différentes sont dissimilaires. Ce partitionnement peut se faire de plusieurs manières. Par exemple en utilisant une mesure de similarité ou de dissimilarité entre les nœuds du graphe, puis en exécutant un algorithme de clustering tel que le k-médoïdes sur base de ces (dis-)similarités.
Ou alors, en travaillant directement sur le graphe en cherchant à détecter des zones denses dans celui-ci. Cela peut se faire via de la propagation de label [17], ou via l’optimisation d’une fonction objectif mesurant la qualité du partitionnement, telle que la modularité. L’algorithme d’optimisation de la modularité le plus célèbre est la méthode de Louvain [18].
Nous avions déjà mentionné l’utilisation des méthodes de partitionnement de graphes dans plusieurs articles de blog [9, 10], ces algorithmes sont utilisés notamment en communication et marketing afin de pouvoir réaliser des annonces ciblées.
- Extraire des caractéristiques ou des représentations.
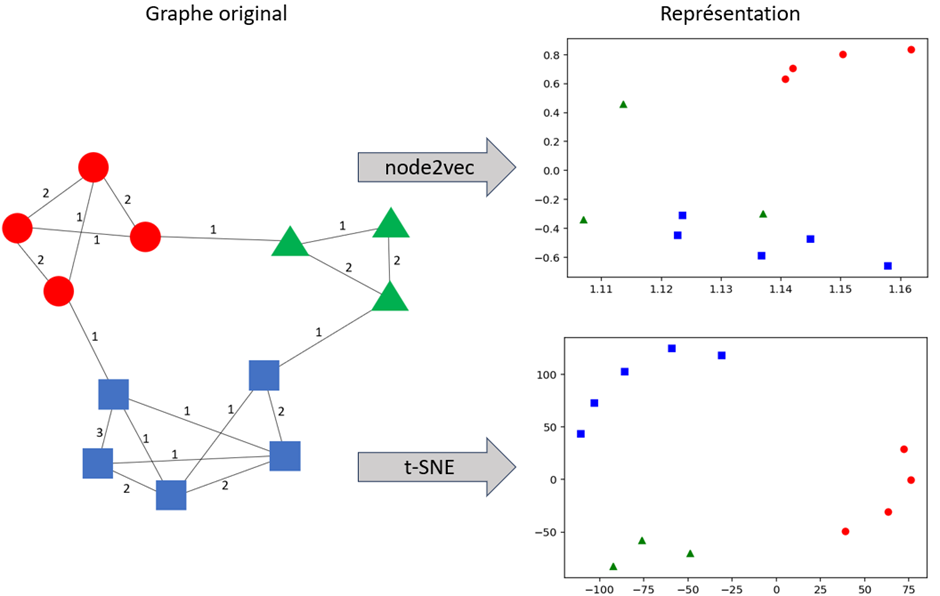
Une des limites des modèles de machine learning classique est qu’ils considèrent uniquement les données (variables continues et catégorielles) relatives aux observations, et ignorent l’information qui pourrait être tirée des relations entre les observations. Si des relations existent entre ces données, un graphe peut être construit, et les modèles de machine learning peuvent être enrichis via l’ajout de nouvelles variables extraites du graphe (il y a aussi un article de blog à ce sujet [11]). Ces nouvelles variables peuvent par exemple être une mesure de centralité (variable continue) ou le résultat d’un partitionnement (variable catégorielle), ou encore être obtenues via des méthodes de graph embedding (variables continues). Le graph embedding vise à obtenir une représentation des nœuds dans un espace multidimensionnel. Cet espace est calculé de sorte que, si deux nœuds sont proches dans le graphe, ils le seront aussi dans cet espace. Cet espace peut par exemple s’obtenir via des méthodes travaillant directement sur le graphe (node2vec [19], fastRP [20]) ou en travaillant sur base de similarités (kernelPCA [21]) ou de distances (t-SNE [22]) par exemple. Voir Figure 3 pour un exemple de représentation en 2 dimensions d’un graphe pondéré simple.
- Prédire des liens.
Le concept de prédiction de lien est relativement explicite, il s’agit d’estimer la probabilité qu’un lien existe entre 2 nœuds. Cela permet de détecter des potentiels arcs manquants (graphe incomplet), ou de prédire l’apparition de nouveaux arcs. Les algorithmes de recommandations sont un exemple courant de prédiction de lien utilisateur-produit, mais ces algorithmes peuvent aussi servir à détecter des potentielles interactions encore inconnues à l’intérieur de réseaux biologiques. Ce genre de prédiction se fait souvent via des méthodes basées sur des similarités entre nœuds, de la factorisation matricielle, des modèles probabilistes ou des réseaux de neurones artificiels [23].
Quels outils ?
Comme mentionné précédemment, la représentation de graphes sous forme matricielle permet de les exploiter de façon efficace via des langages de programmation scientifiques. Cependant, il existe aussi des librairies ou logiciels permettant de créer et exploiter des données de graphe.
Voici quelques exemples de librairies dédiées au travail sur les graphes. Ces librairies permettent de créer un objet graphe, qui peut être construit de plusieurs manières. Il peut être construit à vide, avant d’y ajouter manuellement des nœuds et des arcs, ou alors à partir d’une matrice d’adjacence ou d’une liste d’arcs, ou bien encore directement depuis des fichiers contenant une description du graphe sous la forme d’une liste de nœuds et d’arcs. Quelques exemples de librairies orientées graphe incluent igraph, networkx, graph-tool ou networkit pour Python, igraph pour R et Graphs pour Julia.
Pour un utilisateur ayant déjà des connaissances dans l’un de ces langages, ces libraires ont l’avantage d’être intuitives et faciles à prendre en main, et contiennent de nombreux algorithmes de graphe pré-implémentés.
Il existe aussi de nombreux logiciels prévus pour l’analyse du contenu de bases de données orientées graphe, tels que Gephi ou Cytoscape (pour une liste plus détaillée, nous vous invitons à vous référer à l’un de nos précédents articles sur le sujet : [3]). Il s’agit bien de logiciels créés pour des analyses ponctuelles ou des explorations visuelles des relations dans des ensembles de données, mais qui ne sont pas conçus pour intégrer et gérer de grandes quantités de données de manière continue comme le ferait une base de données orientée graphe.
Conclusion
Dans la première partie de cet article dédié aux différentes technologies basées sur les graphes, nous avons fait une rapide présentation de la théorie des graphes, ainsi que des principaux algorithmes de graphe et leurs applications. La seconde partie se penchera sur les bases de données orientées graphe et les graphes de connaissances, les différences entre ces concepts ainsi que les outils qui y sont associés.
Références
Quelques articles de blog Smals Research concernant les graphes :
[2] Sept (bonnes) raisons d’utiliser une Graph Database
[3] Explorer une base de données orientée graphes
[4] Les graphes de connaissance, incontournable pour l’intelligence artificielle
[5] Les graphes de connaissance : quelques applications
[6] Smals KG Checklist: déterminer si un graphe de connaissances peut résoudre un problème concret
[7] Un fraudeur ne fraude jamais seul
[8] Un fraudeur ne fraude jamais seul, partie 2
[9] Ce qu’un réseau social peut nous apprendre
[10] Facebook : peut-on vraiment cacher sa liste d’amis ?
[11] Améliorer le Machine Learning avec des données graphes
Sources scientifiques :
[12] Katz, L. (1953). A new status index derived from sociometric analysis. Psychometrika, 18(1), 39-43.
[13] Fouss, F., Pirotte, A., Renders, J. M., & Saerens, M. (2007). Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation. IEEE Transactions on knowledge and data engineering, 19(3), 355-369.
[14] Page, L., Brin, S., Motwani, R., & Winograd, T. (1998). The pagerank citation ranking: Bringing order to the web. Technical report, Stanford Digital Libraries.
[15] Gleich, D. F. (2015). PageRank beyond the web. siam REVIEW, 57(3), 321-363.
[16] Kleinberg, J. M. (1999). Authoritative sources in a hyperlinked environment. Journal of the ACM (JACM), 46(5), 604-632.
[17] Raghavan, U. N., Albert, R., & Kumara, S. (2007). Near linear time algorithm to detect community structures in large-scale networks. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics, 76(3), 036106.
[18] Blondel, V. D., Guillaume, J. L., Lambiotte, R., & Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of statistical mechanics: theory and experiment, 2008(10), P10008.
[19] Grover, A., & Leskovec, J. (2016). node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 855-864).
[20] Chen, H., Sultan, S. F., Tian, Y., Chen, M., & Skiena, S. (2019, November). Fast and accurate network embeddings via very sparse random projection. In Proceedings of the 28th ACM international conference on information and knowledge management (pp. 399-408).
[21] Schölkopf, B., & Smola, A. J. (2002). Learning with kernels: support vector machines, regularization, optimization, and beyond.
[22] Van der Maaten, L., & Hinton, G. (2008). Visualizing data using t-SNE. Journal of machine learning research, 9(11).
[23] Lü, L., & Zhou, T. (2011). Link prediction in complex networks: A survey. Physica A: statistical mechanics and its applications, 390(6), 1150-1170.
Ce post est une contribution individuelle de Pierre Leleux, data scientist et network data analyst chez Smals Research. Cet article est écrit en son nom propre et n’impacte en rien le point de vue de Smals.

Leave a Reply