Het tijdperk van de kwantumcomputers lijkt snel dichterbij te komen. Dergelijke computers zouden een mokerslag geven aan de hedendaagse cryptografie. Bedrijven claimen revolutionaire doorbraken. Grootmachten investeren miljarden waardoor het zelfs wat doet denken aan een wapenwedloop. De dominantie van de kwantumcomputer lijkt wel zeer snel realiteit te gaan worden.

Bij bedrijven en overheidsinstellingen groeit samen met de onduidelijkheid ook de ongerustheid. Hoogtijd dus om wat klaarheid te brengen in deze complexe problematiek door middel van een vierdelige reeks Kwantumcomputers en cryptografie! Dit is het eerste deel en gaat in op de basisprincipes van kwantumcomputers.

Klassieke computer stoot op limieten

De wet van Moore – eigenlijk een extrapolatie – stelt dat om de zoveel tijd het aantal transistors op een chip verdubbelt. Oorspronkelijk was dit om de 12 maand, maar het is ondertussen afgevlakt naar 24 maand. Aangenomen wordt dat ze rond 2025 zal ophouden. Krachtigere klassieke computers bouwen wordt meer en meer een uitdaging.

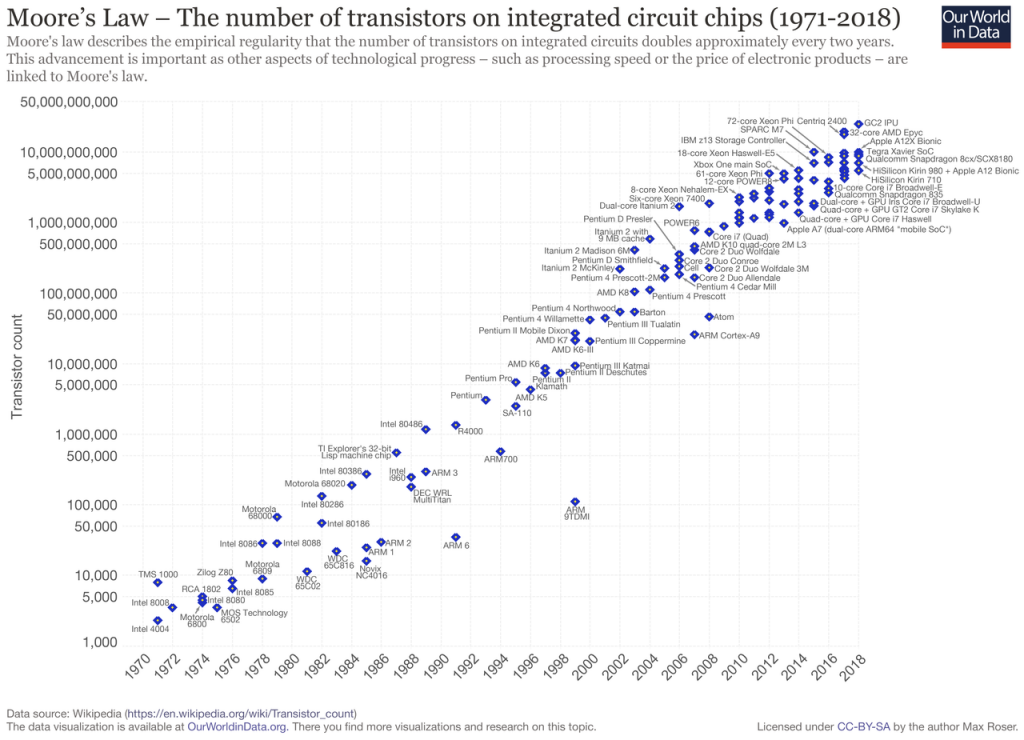
Evolutionair gezien lijkt de opkomst van kwantumcomputers dan ook logisch. Klassieke computers zijn gebaseerd op  Newtoniaanse – dus de klassieke – fysica. Men bouwt daarbij steeds kleinere circuits. Vandaag zijn ze nog nauwelijks enkele nanometers. Als je maar voldoende inzoomt kom je op den duur onvermijdelijk op atomair en subatomair niveau en dus in een wereld waar de kwantumechanische wetten spelen. De kwantumfysica is krachtiger dan de Newtoniaanse en bijgevolg zijn ook kwantumcomputers – in theorie althans – krachtiger dan de Newtoniaanse.

Hoe werkt een kwantumcomputer

Klassieke computers hebben als kleinste informatie- en verwerkingseenheid de bit, die ofwel de waarde 0 ofwel de waarde 1 heeft. Bij kwantumcomputers is de kleinste informatie- en verwerkingseenheid de qubit (quantum bit), wat een klein deeltje is, zoals een foton of elektron, en waar dus de kwantummechanische effecten ten volle spelen en ook benut worden.

Volgens kwantummechanica gedragen kleine deeltjes, zoals elektronen, ionen en fotonen, zich als golven (en vice versa), waarmee bedoeld wordt dat hun toestand – snelheid, positie, spin, polarisatie – ‘uitgesmeerd’ is over de verschillende mogelijke toestanden en daarbij geen specifiek karakter kent. Pas bij het meten neemt deze golf één concrete toestand aan. Een elektron, bijvoorbeeld, krijgt bij het meten één concrete spin (rotatie om zijn as). Men zegt dat de golffunctie bij het meten ineenstort.

Dat brengt ons bij de eerste eigenschap van qubits: de superpositie. De waarde van een qubit is onbepaald tot op het moment van de meting, wat met een bepaalde waarschijnlijkheid 0 als resultaat geeft, en met een bepaalde waarschijnlijkheid 1. Vaak wordt gesteld dat een qubit de waardes 0 en 1 tegelijkertijd heeft, maar een dergelijke formulering maakt de zaken nodeloos complex en mystiek. Pas bij de meting neemt de qubit dus een concrete waarde aan (0 of 1). We zeggen dat de qubit bij de meting ineenstort, aangezien haar toestand niet langer een superpositie (het mogelijke) is maar één concrete waarde (het feitelijke). Het uitlezen van een qubit verstoort dus haar toestand.

Door het probabilistisch karakter zal het meten van verschillende qubits in dezelfde toestand (dus met dezelfde waarschijnlijkheidsdistributie) niet steeds hetzelfde resultaat geven. Volgens de Kopenhaagse – de meest populaire – interpretatie van de kwantummechanica is de uitkomst van een meting volledig ondeterministisch en dus – i.t.t. tot de Newtoniaanse fysica – niet aan de hand van andere factoren te verklaren. Voor Einstein was dit problematisch, wat wordt weergegeven door het populaire, door hem meerdere malen herhaalde citaat “Jedenfalls bin ich überzeugt, daß der nicht würfelt.” (“Ik ben er in elk geval van overtuigd dat Hij [God] niet dobbelt.”)

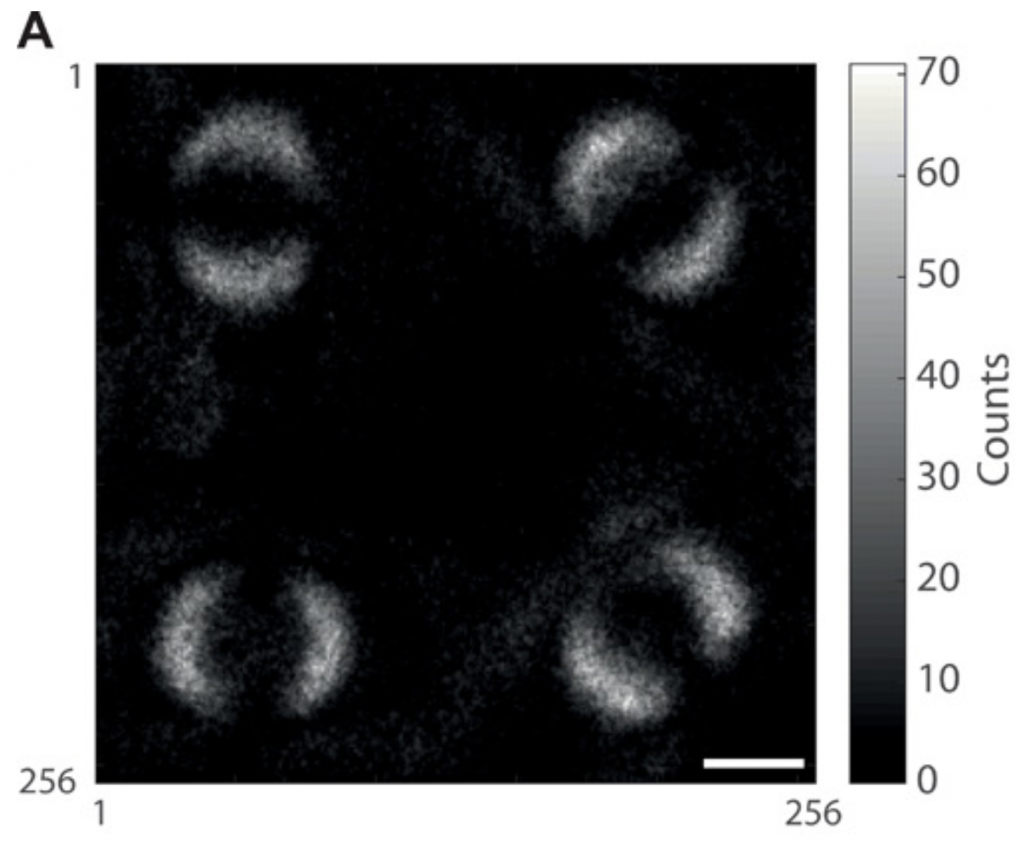
Een tweede kwantumeigenschap is de verstrengeling (entanglement), wat wil zeggen dat er een correlatie bestaat tussen de metingen van twee of meerdere verwante deeltjes, waarbij de fysieke afstand tussen de deeltjes er niet toe doet. Als twee qubits verstrengeld zijn met een gelijke superpositie dan weten we dat beide qubits bij lezing dezelfde waarde zullen teruggeven. We hoeven dus maar één qubit te lezen om te weten wat het resultaat zou zijn bij lezing van de andere qubit.

Dit lijkt in tegenspraak met wat eerder gezegd is, namelijk dat de uitkomst van een meting volledig ondeterministisch is. Experimenteel werd echter reeds met hoge waarschijnlijkheid aangetoond dat de correlatie niet te verklaren is aan de hand van lokale variabelen en dat er dus hoogstwaarschijnlijk een soort connectie tussen de deeltjes is, onafhankelijk van hun afstand. Dit is tegenintuïtief en strijdig met de Newtoniaanse fysica, waarbij afstand wel degelijk een cruciale rol speelt bij de invloed die objecten op elkaar uitoefenen. Zelfs Einstein had het er moeilijk mee en noemde dit vreemde verschijnsel spottend “spukhafte Fernwirkung” (“spookachtige werking op afstand“). Voorlopig moeten we dit, gegeven de ondertussen sterke experimentele bevestiging, aanvaarden als meest waarschijnlijke hypothese.

Kwantumberekeningen

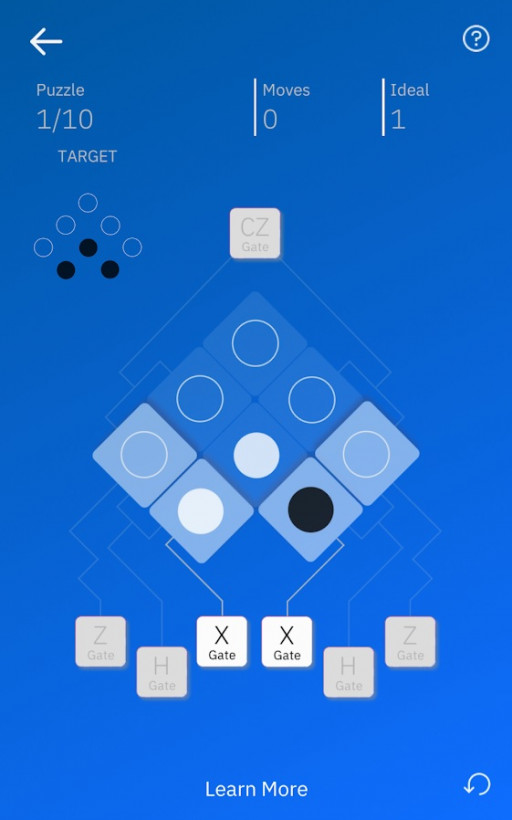
Berekeningen met klassieke bits gebeuren op het laagste niveau met behulp van logische poorten, zoals de NOT, AND en OR poort. Het manipuleren van één, twee of een beperkt aantal qubits gebeurt daarentegen met behulp van kwantum logische poorten (die beschreven worden door matrixoperaties met complexe getallen). De Pauli-X poort in de kwantumwereld komt bijvoorbeeld overeen met de NOT poort bij klassieke computers. Na het toepassen van de Pauli-X poort op een qubit verwisselen de waarschijnlijkheden (meer correct, de amplitudes) om 0 en 1 te meten. Daarnaast zijn er nog vele andere poorten, zoals de Hadamard poort die gebruikt wordt om (sets van) qubits te initialiseren. Een toegankelijke intro tot het manipuleren van qubits met behulp van kwantum logische poorten is de Hello Quantum app van IBM, die zowel voor iOS als Android beschikbaar is. Het wordt gepresenteerd als een spelletje waarbij je puzzels moet oplossen om naar een hoger niveau te gaan.

Kwantumalgoritmes zijn dus gebouwd op een totaal andere logica dan die voor klassieke computers. Ze vereisen dan ook specifieke assembleertalen, programmeertalen en ontwikkelomgevingen (Software development kits). Enkele kwantum assembleertalen zijn Quil en OpenQASM. Voorbeelden van kwantum programmeertalen zijn Quantum Computation Language (QCL), Q# en Q language. Bestaande ontwikkelomgevingen zijn o.a. Qiskit, ProjectQ en Forest en zijn vandaag vaak gebaseerd op bestaande  programmeertalen zoals Python.

De populaire perceptie dat de kwantumcomputer in alles de klassieke computer zal verslaan is trouwens fout. Voor het overweldigende deel van computerberekeningen bieden kwantumcomputers geen performantiewinsten ten opzichte van klassieke computers. Het is een populaire misvatting dat kwantumcomputers alle problemen zullen kunnen oplossen die moeilijk (of zelfs onmogelijk) zijn voor klassieke computers.

Er is weliswaar een beperkte, maar zeer interessante, categorie van problemen waar kwantumcomputers in excelleren. Daaronder vinden we problemen die moeilijk zijn voor klassieke computers en sowieso moeilijk moeten blijven om de moderne cryptografie veilig te houden. Anders gezegd zullen voldoende krachtige kwantumcomputers een groot deel van de moderne cryptografie kunnen kraken. Dit verklaart meteen ook grotendeels de investeringen van grootmachten zoals China en de VS in de technologie. De beveiligde communicatie van de tegenstander kraken is altijd al zeer interessant geweest en heeft in de Tweede Wereldoorlog trouwens niet enkel geleid tot een cruciale wending, maar ook tot de ontwikkeling van de klassieke computer.

Verder wordt ook naar kwantumcomputers gekeken voor optimalisatieproblemen, simulaties en machine learning, maar dit valt buiten de scope van deze – toch al uitgebreide – artikelenreeks.

Kwantumcomputers zijn bovendien probabilistisch en geven dus enkel met hoge waarschijnlijkheid correcte resultaten.

Conclusie

Samengevat maken kwantumcomputers gebruik van weinig intuïtieve kwantummechanische effecten zoals superpositie en verstrengeling. Daarmee steunt het op fundamenteel andere – en krachtigere – principes dan klassieke computers.

Toch blijft er nog veel onduidelijkheid over het potentieel. Koen Bertels, een Belgische professor aan de TU Delft en hoofd van het Quantum Computer Architectures Lab aan diezelfde universiteit stelde recent: “Hoeveel keer sneller [kwantumcomputers zullen zijn] is echter nog koffiedik kijken. Misschien 10 keer, misschien 100 keer. Sommigen hebben het zelfs over 100 miljoen keer sneller.”

Het grote voordeel dat een krachtige klassieke computer vandaag nog geniet ten opzichte van een krachtige kwantumcomputer is dat hij effectief bestaat. Maar dat kan natuurlijk ooit veranderen. Bereiden we ons dan toch alvast niet best voor op een tijdperk?

Deel 2 van deze reeks zal daarom ingaan op de bouw van kwantumcomputers: Waar staan we vandaag en waarom is het zo moeilijk? Deel 3 bespreekt de impact op de moderne cryptografie. Deel 4, ten slotte, bekijkt hoe de cryptografische wereld zich tegen de kwantumdreiging kan wapenen.

---

Dit is een ingezonden bijdrage van Kristof Verslype, cryptograaf bij Smals Research. Het werd geschreven in eigen naam en neemt geen standpunt in namens Smals.