Dans le premier article de notre série consacrée à l’analyse réseau du marché du travail en Belgique, nous avons présenté les données constituant le graphe (ou réseau) de Dimona, sur lequel se base cette série de trois articles, et montré quelques métriques, permettant par exemple d’évaluer le nombre de personnes actives à un moment donné, ou le nombre d’employeurs par travailleurs et vice-versa.

Dans le second article, nous avons vu que le graphe pouvait être découpé en sous-graphes, soit en considérant les composantes connexes, soit en y calculant des communautés.

Dans ce troisième et dernier article, nous allons nous intéresser dans un premier temps à la notion d’homophilie, pour ensuite parler du concept de projection d’un graphe (biparti).

Homophilie

En sociologie, le terme “homophilie” (déjà exploité dans un blog précédent) désigne le fait pour une personne d’avoir plus d’affinité avec les personnes similaires à elle-même (“qui se ressemble s’assemble”). Par extension, en théorie des réseaux, on dira qu’un réseau est homophile si, dans le voisinage immédiat d’un nœud, on aura tendance à trouver des nœuds similaires à ce nœud. La notion de similarité peut vouloir dire beaucoup de choses : pour des personnes, partager des centres d’intérêts, une ethnie, un niveau de formation ou socio-économique, une religion… pour des entreprises, être actif dans le même secteur, dans la même région, voire même être également enclins à frauder.

Nous allons ici voir dans quelle mesure le marché du travail belge est “homophile”, et cela selon deux caractéristiques : la province de l’employeur, et ses codes NACE. Nous nous poserons donc la question suivante : un travailleur employé par une société située en province X (ou exerçant dans le domaine X) va-t-il, s’il change d’employeur, favoriser une entreprise de la même province (ou du même domaine) ?

Homophilie par province

Aperçu général

En premier lieu, nous allons évaluer, pour chaque province, la proportion de travailleurs qui travaillent dans cette province, puis changent de travail pour un employeur dans une autre province. Le nombre obtenu pourrait ainsi être interprété comme une mesure de la “fidélisation” d’une province.

Il nous faut donc calculer deux valeurs pour chaque province :

• Le nombre de personnes qui, sur la période étudiée, y ont eu un emploi
• Le nombre de personnes qui, après un emploi dans cette province, ont trouvé un emploi dans une autre.

Requêtes Cypher

MATCH (c:Company)--(p:People)
RETURN c.Province, COUNT(DISTINCT p)

MATCH (c1:Company)-[r1]-(w:People)-[r2]-(c2:Company) 
WHERE 
   c1 <> c2 
   AND r1.START <= r2.START 
   AND coalesce(c1.Province, "null") <> c2.Province
RETURN c1.Province, COUNT(DISTINCT p)

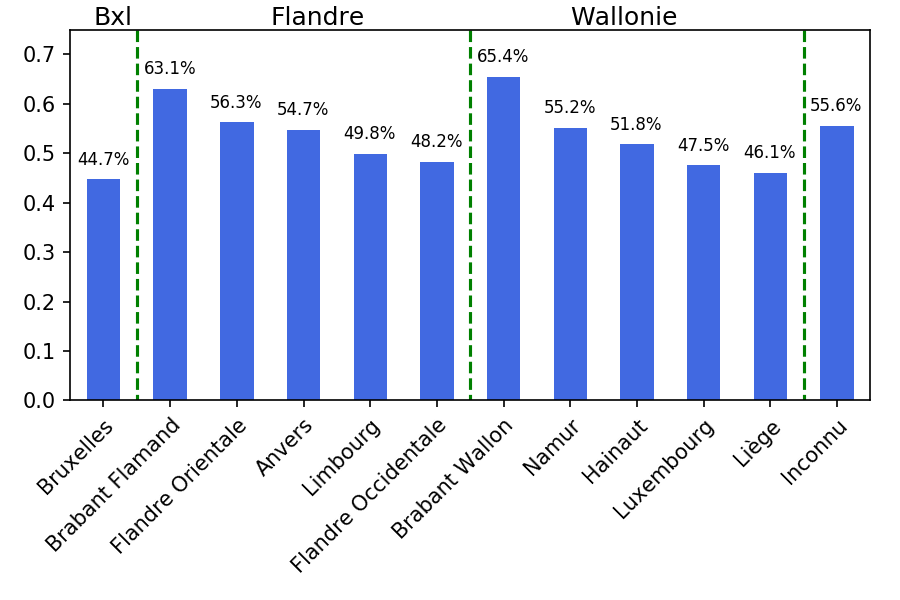
Combinées, ces données nous permettent d’obtenir le graphique suivant :

Notons que la colonne “Bruxelles” est particulière : c’est dans la capitale que la plupart des entreprises actives sur tout le territoire (ministères, chaînes de magasins…) ont leur siège social. Le fait que son employeur soit renseigné à Bruxelles ne veut donc pas dire que l’on travaille dans cette ville.

Le graphique nous indique que 63% des personnes ayant travaillé dans le Brabant Flamand ont ensuite trouvé un emploi ailleurs, alors que seuls 46 % des travailleurs liégeois ont quitté leur province. En termes d’homophilie, on peut donc estimer que Liège est plus “homophile” que le Brabant Flamand : dans le “voisinage” de Liège (les autres employeurs des travailleurs d’employeurs liégeois), on trouve une plus grande proportion d’entreprises Liégeoises qu’on ne trouve d’entreprises (flamo-)brabançonnes dans le voisinage du Brabant Flamand.

Notons que ce constat ne dit rien des raisons : les liégeois ne sont pas nécessairement “pantouflards”, il se peut que les conditions de travail y soient si bonnes que rares sont ceux qui veulent aller voir ailleurs.

Aperçu détaillé

Si l’on veut une vue plus détaillée de cette notion d’homophilie provinciale, on peut aussi comparer, pour chaque province P, les deux répartitions suivantes :

• La répartition du voisinage de P, c’est-à-dire les provinces où travaillent tous les travailleurs qui ont d’abord travaillé pour une entreprise situé en province P
• La répartition générale des travailleurs par province.

Pour la répartition générale, nous allons calculer le nombre de personnes ayant eu, au cours de ce 15 dernières années, un emploi dans chaque province.

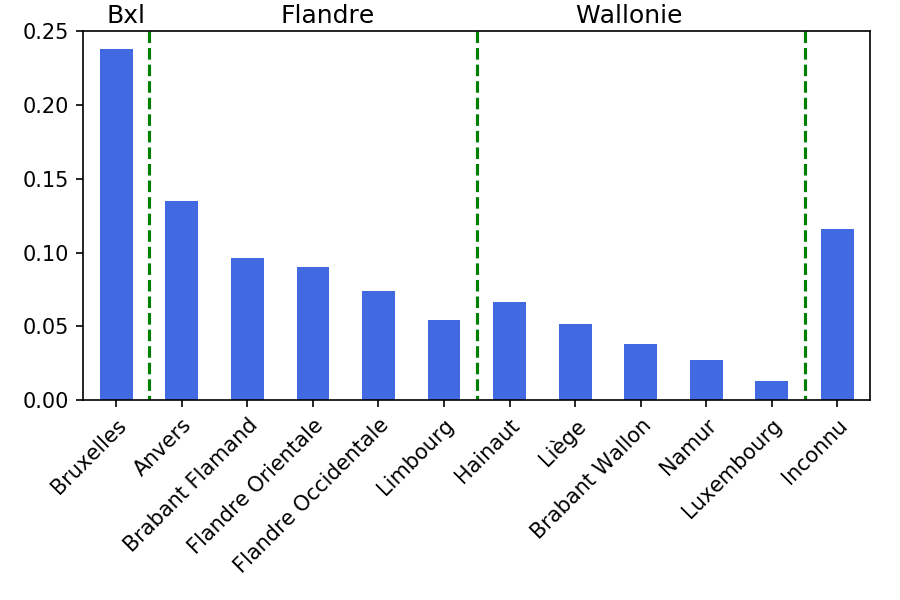
Comme nous souhaitons obtenir une distribution, la somme de toutes nos colonnes doit être égale à 1 (ou 100%). Nous divisons donc chaque colonne par la somme de toutes les colonnes. Cette valeur est supérieure à la population totale, car chaque travailleur ayant travaillé dans deux provinces sera compté 2 fois. Ce qui compte, ce n’est pas la hauteur absolue d’une colonne, mais sa hauteur par rapport aux autres colonnes.

Nous obtenons le graphique ci-contre.

Requêtes Cypher

MATCH (c:Company)--(p:People)
RETURN c.Province, COUNT(DISTINCT p)

Nous calculons ensuite, pour chaque province P, le nombre de personnes qui, après un emploi dans cette province P, ont eu un autre emploi dans cette même province, ce qui nous donne la série de graphiques ci-dessous.

Requête Cypher

MATCH (c1:Company)-[r1]-(p:People)-[r2]-(c2:Company) 
WHERE c1 <> c2 AND r1.START <= r2.START
RETURN c1.Province, c2.Province, COUNT(DISTINCT p)

Notons qu’il est difficile de comparer la vue générale que nous avons montrée ci-dessus avec cette série de graphiques, pour plusieurs raisons :

• La série de graphiques montre comment se sont comportés ceux qui ont changé de travail. On ne compte donc pas ceux qui n’ont jamais changé d’employeurs, ce qui représente un peu plus de 42 % des travailleurs, comme mentionné dans notre premier blog .
• Un travailleur qui a d’abord travaillé à Bruxelles, pour ensuite partir à Namur et puis à Mons, en Hainaut, sera repris à la fois dans les transferts Bruxelles-Namur, mais également Bruxelles-Hainaut. On ne peut donc pas sommer les migrations entre une province et les autres pour connaitre le nombre de personnes ayant quitté la province.
• Si la hauteur absolue d’une colonne dans le graphique général a un sens (proportion de travailleurs ayant quitté la province), elle n’en a pas vraiment la série de graphiques qui suit.

Quelques observations peuvent être faites :

• La répartition du voisinage de Bruxelles diffère peu de la répartition globale des travailleurs : cela s’explique très probablement par ce qui a déjà été évoqué, la plupart des grandes structures ayant leur siège social à Bruxelles
• En dehors de Bruxelles, le voisinage d’une province reste majoritairement dans la même région (Flandre ou Wallonie)

Homophilie par secteur (Code NACE)

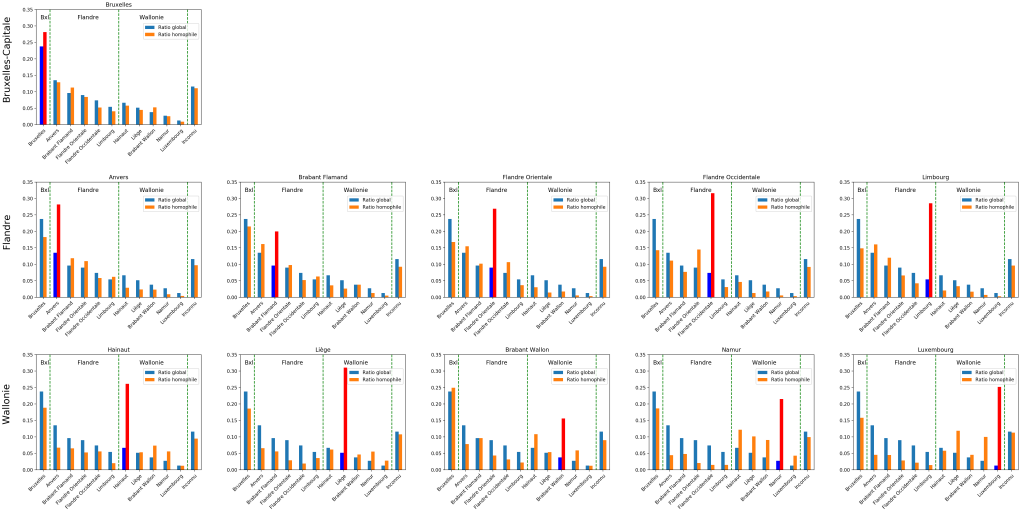
Nous avons réalisé une analyse similaire sur base des Code NACE (décrits dans notre premier article), précisant le secteur d’activité, à nouveau en excluant les contrats d’intérim. Nous nous posons la question suivante : le “voisinage d’un secteur” (à savoir les entreprises dans lesquelles travaillent les travailleurs d’entreprises du dit secteur) est-il différenciable de l’ensemble de la population des entreprises ?

Nous présentons pour ce faire les graphiques accessibles dans ce document joint.

Pour chaque page, correspondant à un code NACE (de premier niveau), on trouve sur la première ligne la comparaison entre la distribution des codes NACE des entreprises en général (en bleu) et la distribution des entreprises employant au moins un travailleur ayant été embauché par une entreprise du code NACE concerné. À gauche, la comparaison se fait sur base du nombre d’entreprises. À droite, sur base du nombre de travailleurs. En titre, le coefficient de correlation (selon la méthode de Pearson) indique à quel point le voisinage du secteur analysé diffère de la distribution globale. Proche de 1, il sera quasiment indifférenciable, plus on s’en éloigne, plus spécifique sera le voisinage du secteur analysé.

Les graphiques du bas, indiquent, pour chaque code NACE, le ratio entre les deux colonnes du graphique du haut. Il s’agit d’une autre façon de voir les secteurs surreprésentés (au dessus de la ligne pointillée rouge) et sous-représentés (en dessous de la ligne).

Nous constatons que pour quasiment tous les secteurs, ce même secteur est sur-représenté dans le voisinage, montrant que le phénomène d’homophilie est observé. La sur-représentation présente cependant des grandes variations : à peine perceptible pour le commerce (code G), très importante pour des secteurs très spécialisés (et concernant très peu de monde), comme les activités extra-territoriales (code U) ou l’extraction (code B).

Nous laissons au lecteur le choix d’aller plus loin dans l’analyse, en identifiant par exemple des secteurs “associés” (souvent sur-représentés ensemble).

Projection biparti

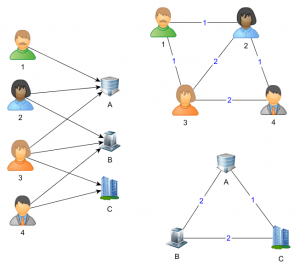
Graphe biparti (à gauche), représentant les liens entre employés et employeurs, et ses deux projections biparti (à droite), représentant le réseau des collègues (en haut) et le réseaux des employeurs (en bas). Les poids, en bleu, indiquent respectivement le nombre d’employeurs et d’employés en commun.

Lorsque l’on a un graphe biparti, c’est-à-dire un graphe avec deux types de nœuds A et B (comme par exemple travailleur et employeur) et des arcs qui vont uniquement entre un nœud du type A et un nœud du type B (comme par exemple les relations de travail), on peut réaliser ce qu’on appelle une projection biparti. Il s’agit d’un graphe qui ne comportera que des nœuds d’un type A (resp. B), et qui aura un arc entre deux nœuds x₁ et x₂ s’il existe dans le graphe d’origine un nœud du type B (resp. A), lié à x₁ et à x₂. Il existe toujours deux projections d’un graphe biparti : une pour chaque type de nœud. Dans le cas qui nous occupe, nous aurons un graphe reprenant la totalité des employeurs, et un lien entre deux employeurs s’il existe une personne ayant travaillé pour les deux employeurs, et un graphe reprenant la totalité des travailleurs, avec un lien entre deux travailleurs s’ils ont un jour été collègue (en supposant deux personnes collègues si elles ont travaillé pour un même employeur, mais pas nécessairement en même temps).

Les arcs créés dans la projection biparti sont souvent associée à un poids, qui peut par exemple avoir pour valeur le nombre de nœuds “compressés” dans la projection : il peut s’agit du nombre de travailleurs partagés dans le cas de la projection sur les employeurs, ou du nombre d’entreprises dans lequel les deux extrémités de la relation ont été collègues.

Pour l’analyse qui suit, nous n’avons pas considéré les travailleurs intérimaires, qui, par nature, changent souvent d’employeurs, et pourraient fausser les impressions. Nous n’avons par ailleurs considéré que la composante géante (voir notre article précédent). Par définition, il n’y aura pas de travailleurs en commun entre deux entreprises faisant partie de deux composantes connexes distinctes.

Nous n’avons pas pu réaliser l’analyse qui suit dans la base de donnée Neo4j, n’ayant trouvé aucune fonctionnalité permettant de réaliser les projections voulues. Nous avons utilisé la librairie igraph.

Projection par entreprise

La première projection que nous avons réalisée est la projection par entreprise. Elle comporte un peu plus de 530 000 employeurs, et 22 millions de liens. En regardant le poids de ces liens (indiquant dont le nombre de travailleurs partagés), on en trouve 18.6 millions ayant la valeur 1. Il y a donc 18.6 millions de couples d’employeurs ne partageant qu’un seul travailleur. Les valeurs les plus intéressantes se trouvent à l’autre extrémité : il existe deux employeurs se partageant 37 350 travailleurs ! Nous y trouvons ensuite un triplet d’employeurs qui se partagent deux par deux, respectivement, 11 000, 10 000 et 7 000 travailleurs.

Le premier est le fait d’une société nationale, qui a une structure juridique séparée pour la gestion de ses ressources humaines. Chaque travailleur y est déclaré dans les deux structures. Le second concerne un organisme de gestion d’artistes, divisé en plusieurs structures juridiques distinctes. On trouve aussi un chaîne de grands magasins de près de 140 000 salariés (dont un très grand nombre de jobistes), partageant 5 800 travailleurs avec un ministère de 250 000 salariés. Il n’est bien sûr pas surprenant que deux aussi gros employeurs partagent autant de personnel. L’essentiel de ce que l’on voit par la suite est du même acabit : de très gros employeurs, liés entre eux par un nombre de salariés qui est dans l’absolu élevé, mais pas relativement au nombre d’employés respectif. Une analyse plus approfondie, où l’on placerait en poids la proportion de personnel partagé (par exemple, avec la distance de Jaccard) apporterait un autre éclairage. On pourrait par exemple détecter des transferts d’entreprises, des rachats ou des fusions. Nous n’irons pas plus loin ici dans cette analyse.

Projection par travailleur

La projection par travailleur pose un problème de taille : elle est très largement plus volumineuse que celle par entreprise. Nous sommes parvenus à déterminer qu’elle devait comporter un peu plus de 7 millions de nœuds, et pas loin de 400 millions d’arcs, mais, en utilisant la libraire igraph sur un serveur ayant à sa disposition 64 GB de mémoire, nous n’avons pas réussi à la calculer. Cependant, nous voulions principalement mettre en évidence les couples de personnes partageant de nombreux employeurs.

Cliquer ici pour voir comment nous avons malgré tout pu contourner cette limitation

Dès lors, nous pouvions d’entrée de jeu éliminer de nos données tous les employeurs ayant moins de deux travailleurs. En effet, un employeur avec un seul travailleur ne pourra par définition pas être un employeur commun entre deux personnes. Cette simplification n’aura aucun impact sur la projection, ces employeurs supprimés n’étant jamais considérés comme “en commun” entre deux travailleurs, et donc n’apparaissent dans aucun poids.

Simplification d’un graphe avant projection. Les noeuds “i” et “3” sont supprimés. À droite : les projections originale (en haut) et simplifiée (en bas).

Dans le même ordre d’idée, si nous voulons trouver tous les couples de travailleurs partageant au moins, mettons, 10 employeurs, nous pouvons également éliminer tous les travailleurs ayant moins de 10 employeurs (pour avoir 10 employeurs en commun avec un autre travailleur, il faut avoir soi-même au moins 10 employeurs). Cette dernière simplification supprimera des nœuds dans la projection résultante, mais uniquement des nœuds qui, dans la projection, ne seront liés à aucun nœud avec un poids supérieur ou égale au seuil fixé (10 dans notre exemple). L’illustration ci-dessous montre un graphe biparti (vert et orange), pour lequel on veut réaliser la projection “verte”, avec un seuil fixé à 4.

Avec la première simplification, le nœud orange “i” (degré = 1, inférieur à 2) est supprimé. Avec la seconde simplification, le nœud vert “3” (degré = 3, inférieur au seuil 4) est supprimé lui aussi. Les deux projections (complète et simplifiée) sont ensuite montrées sur la droite. On y voit qu’en dehors de la suppression du nœud 3, les poids sur les arcs sont identiques.

Le résultat de cette projection nous montre que bon nombre de travailleurs partagent un grand nombre d’employeur avec d’autre salariés. Par exemple, 32 couples de travailleurs (au total, 24 travailleurs), partagent deux par deux plus de 30 employeurs (jusqu’à 46), comme illustré ci-dessous, où chaque nœud représente un travailleur, et les labels sur les arcs le nombre d’employeurs commun entre deux travailleurs.

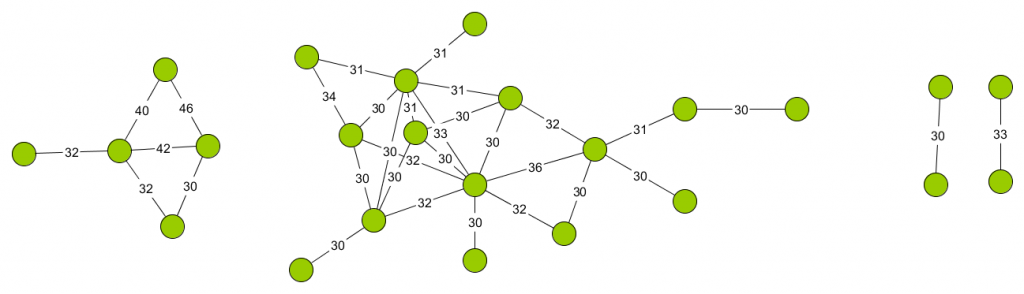
Projection par travailleur, en fixant un seuil à 30 (on ne garde donc que les travailleurs partageant 30 employeurs en commun ou plus). Chaque nœud représente un travailleur, le label sur les arcs indique le nombre d’employeurs en commun.

Une analyse plus approfondie ce ces différents clusters mets en avant certains secteurs : le cluster de gauche concerne des employés embauchés essentiellement en tant que travailleurs occasionnels dans le secteur de la collecte de fruits et légumes ; celui du milieu des entreprises des arts du spectacles. Il s’agit de deux secteurs pour lesquels on change fréquemment d’employeur entre chaque “prestation” (une saison de collecte ou une tournée de spectacle).

Pour chacune des relations affichées sur le réseau ci-dessus, nous avons également calculé la distance de Jaccard, qui indique le ratio entre le nombre de voisins communs entre deux nœuds, et le nombre total de voisins de ces deux nœuds. Il se situe à chaque fois entre 25 et 45 %. Ceci indique que nous ne sommes donc pas dans une situation similaire à celle évoquée ci-dessus (pour la projection par employeur), ou deux “super-employeurs” avaient toutes les chances de partager quelques salariés, mais bien dans des situations ou deux travailleurs partagent une partie importante de leurs employeurs. Il y a donc fort à parier que, dans beaucoup de cas, il s’agisse de personnes qui cherchent du travail ensemble. Ceci pourrait être corroboré en menant une analyse plus fine, et en ne considérant qu’un employeur n’est commun entre deux travailleurs que si les périodes d’engagement coïncident. Nous avons mené cette observation manuellement pour les relations les plus fortes, et observé que c’était le cas dans la majorité des relations de travail.

Conclusions

Cette série d’articles a mis en lumière la puissance que l’analyse réseau, en combinaison avec une base de données orientée graphes, pouvait offrir. La gamme de résultats est très large : on peut à la fois obtenir des métriques offrant une vue très générale (le nombre de travailleurs à un moment donné, le nombre moyen d’employeurs par travailleur…), mais également isoler facilement des comportements qui sortent du lot (travailleurs changeant anormalement souvent d’employeur, employeurs ayant du personnel extrêmement fidèle…). L’analyse réseau est donc à la fois un excellent complément de l’analyse statistique classique, mais est également un outil de très grande valeur pour détecter la fraude ou les erreurs et autres problèmes de qualité dans les données.

Il va de soi que, en combinaison avec des experts soit du marché de l’emploi, soit en statistiques, de nombreuses autres observations pourraient être faites. Certaines de celles-ci pourraient également être obtenues avec des techniques statistiques classiques, mais beaucoup nécessiteraient un travail démesuré, voire même seraient tout simplement impossibles.