La technologie quantique est-elle le futur du XXI^e siècle? C’est la question que se posent nombre de scientifiques à l’heure actuelle. Malgré cette incertitude, la plupart sont d’accord sur un point : la technologie quantique va amener une révolution scientifique sans précédent.

En ce qui concerne la sécurité informatique, la technologie quantique est la bombe à retardement qui va casser une grande partie des algorithmes cryptographiques (AES, RSA, ECC, etc.) utilisés dans les systèmes exploités par la majorité des citoyens quotidiennement (communications, banque, protection des données, etc.).

Les attaques quantiques

Comme déjà expliqué dans un article précédent, les systèmes cryptographiques modernes sont généralement basés sur des problèmes mathématiques dits “durs”, ou “computationally infeasible” en anglais, c’est-à-dire qui n’admettent aucune solution efficace pour résoudre le problème. Par exemple, la sécurité de RSA repose sur le problème de la factorisation entière en nombres premiers : il est facile d’obtenir le produit de deux grands nombres premiers, par contre il est beaucoup plus difficile de trouver les facteurs premiers de celui-ci. Pour visualiser la difficulté du problème, prenons un premier exemple où le produit à factoriser est 91 : il n’est pas trop difficile de retrouver que 91 = 7*13 car ce sont de petits nombres. Maintenant, si nous prenons le nombre appelé RSA-1024 ci-dessous comme deuxième exemple, alors personne à l’heure actuelle n’a été capable de retrouver ses deux facteurs premiers. Jusqu’en 2007, la compagnie RSA Security offrait d’ailleurs 100 000 $ à la première personne réussissant l’exploit.

RSA-1024 = 135066410865995223349603216278805969938881475605667027524485143851526510604859533833940287150571909441798207282164471551373680419703964191743046496589274256239341020864383202110372958725762358509643110564073501508187510676594629205563685529475213500852879416377328533906109750544334999811150056977236890927563

Tout ceci est vrai lorsqu’on utilise des ordinateurs digitaux standards. Or la technologie quantique a complètement changé la donne à ce niveau-là : en effet, il existe aujourd’hui des méthodes exploitant les propriétés mécaniques de la technologie quantique sachant résoudre bon nombre de problèmes dits “durs”. Les deux plus connues sont les algorithmes de Shor et de Grover.

Algorithme de Shor

Cet algorithme a été créé en 1994 par Peter Shor, et il résout le problème de factorisation entière en nombres premiers en un temps polynomial, c’est-à-dire que le problème est considéré comme “faisable”. Ainsi, l’algorithme de Shor est capable de retrouver la factorisation de n’importe quel nombre utilisé par RSA en un temps réaliste. Le système cryptographique RSA est donc complètement cassé avec l’algorithme de Shor.

ALGORITHME DE Grover

Cet algorithme a été créé en 1996 par Lov Grover, et il résout le problème d’inversion de fonction en un temps sous-linéaire. Pour comprendre ce que cela veut dire clairement, prenons un exemple simple: la recherche dans un annuaire. 

Soit X le nom d’une personne, Y=F(X) le numéro de téléphone de cette personne X, et F la fonction qui représente l’annuaire (i.e. l’association d’un nom avec un numéro de téléphone). Avec cet annuaire, il est bien sûr très facile de retrouver Y sachant X : il suffit de chercher directement X, suivant l’ordre alphabétique, et on retrouve Y.

Par contre, ce même annuaire n’est pas trié par numéro de téléphone. Donc si on a un numéro de téléphone Y, alors il est très difficile de retrouver le nom X correspondant. En moyenne, pour un annuaire de 10 000 entrées, il faudra 5 000 essais avant de trouver le nom X. Donc pour N entrées, il faudra N/2 essais.

L’algorithme de Grover, lui, est capable de retrouver le nom X avec seulement √N essais. Donc pour un annuaire de 10 000 entrées, il lui faudra 100 essais ; et pour un annuaire de 25 millions d’entrées, il lui faudra seulement 5 000 essais.

Ce gain de temps est considérable en sécurité informatique. Il permet à l’algorithme de Grover de retrouver de façon très efficace n’importe quelle clé cryptographique utilisée dans les systèmes de chiffrement symétrique supposés sûrs (p.ex. AES) par les agences de sécurité internationales (p.ex. le NIST aux USA).

La cryptographie post-quantique

Même si à l’heure actuelle, il n’existe aucun ordinateur quantique permettant d’exécuter de façon efficace les algorithme de Shor et de Grover, la communauté scientifique cherche déjà à se prémunir des attaques quantiques.

Hash-based cryptography

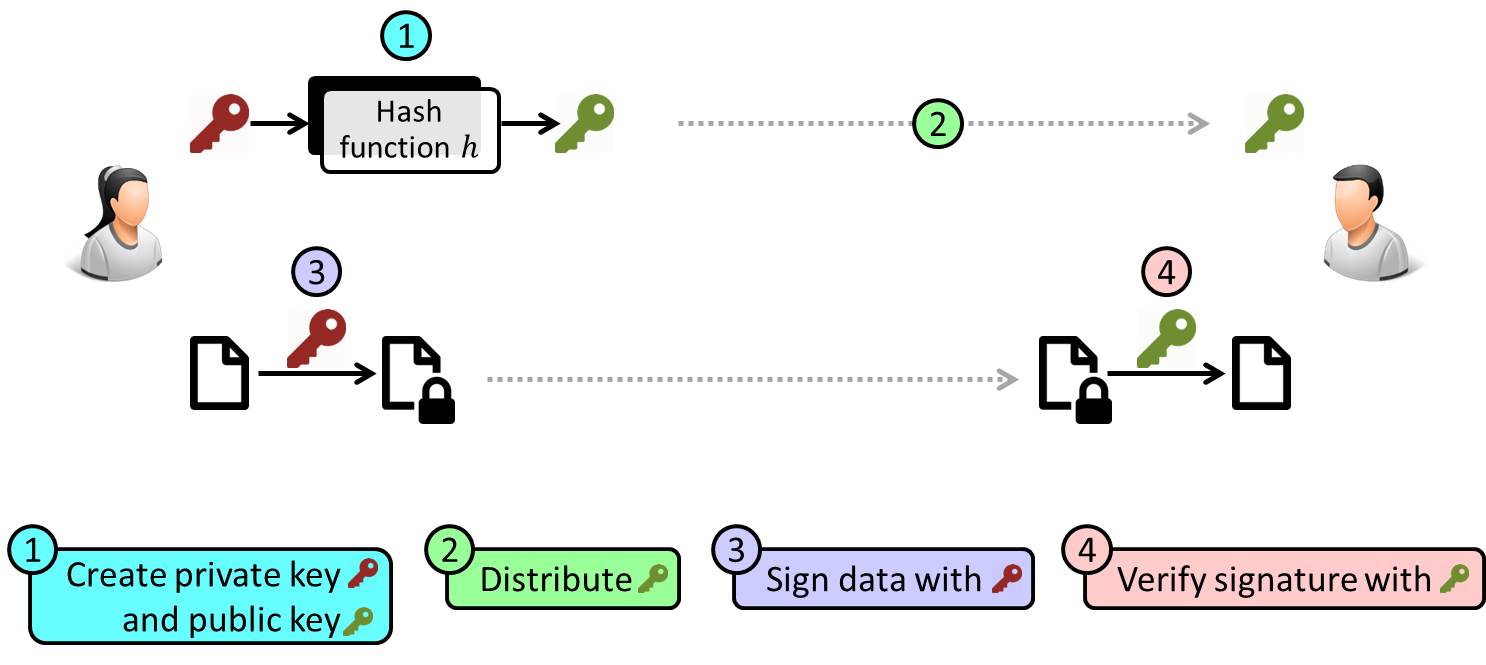
La cryptographie basée sur les fonctions de hachage est une des méthodes les plus intéressantes comme alternative pour des schémas de signature électronique tels que RSA, DSA, ECDSA. En effet, en choisissant des clés cryptographiques suffisamment longues, ce type de cryptographie est résistant à l’algorithme de Grover. Notez qu’il faut quand même doubler la taille des clés pour assurer un bon niveau de sécurité face à la menace quantique.

Les principes de ce type de cryptographie sont détaillés dans la figure ci-dessus. Premièrement, Alice va choisir une clé privée et générer la clé publique correspondante avec une fonction de hachage h qu’elle va communiquer à Bob. Puis Alice va signer un document à l’aide de sa clé privée et envoyer le document signé à Bob. Ce dernier va simplement utiliser la clé publique d’Alice pour vérifier la validité de la signature.

Code-based cryptography

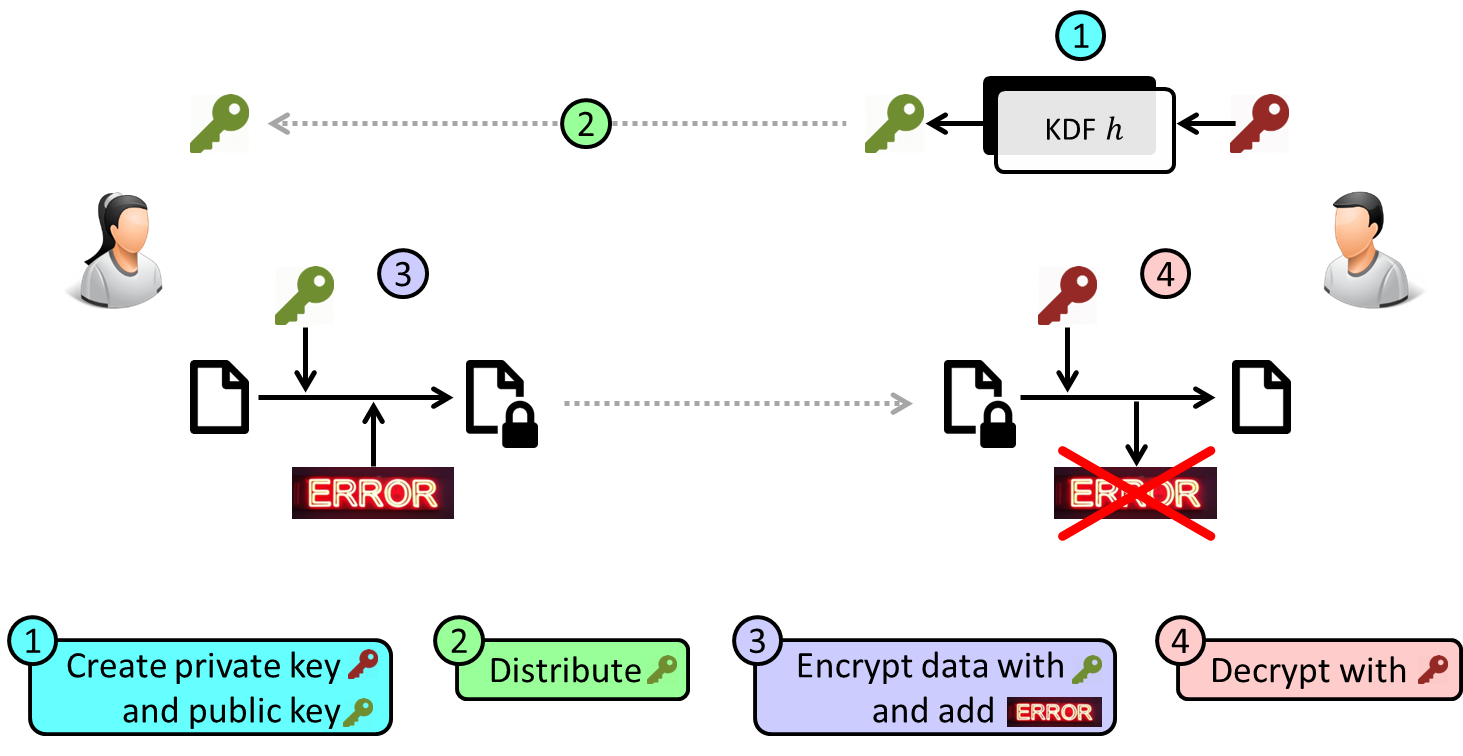
La cryptographie basée sur les codes correcteurs d’erreurs est une méthode assez ancienne (1978 avec le système de chiffrement de McEliece), mais l’intérêt de la communauté scientifique pour cette dernière est relativement récente. En effet, elle est connue aujourd’hui comme étant une alternative intéressante aux chiffrements asymétriques tels que RSA et ECC, tout en étant résistante aux attaques quantiques. Elle aussi nécessite des clés cryptographiques très longues pour résister à l’algorithme de Grover.

Les principes de ce type de cryptographie sont détaillés dans la figure ci-dessus. Premièrement, Bob va choisir une clé privée et générer la clé publique correspondante avec une KDF (Key Derivation Function) h qu’il va communiquer à Alice. Ensuite, Alice va chiffrer un document à l’aide de la clé publique de Bob tout en rajoutant volontairement des erreurs dans le chiffrement. Lorsque Bob va recevoir le document chiffré, il va utiliser sa clé privée pour déchiffrer le document. Comme l’algorithme de chiffrement/déchiffrement est spécialement conçu pour ajouter et enlever correctement les erreurs mises dedans, Bob va tout simplement retrouver le document déchiffré correct.

Il existe bien d’autres méthodes de cryptographie post-quantique. On peut citer la cryptographie multivariate ou la cryptographie basée sur les réseaux (“lattice-based cryptography” en anglais), cette dernière suscitant un grand élan de recherche dans le milieu académique, comme le prouve le site pqcrypto.org fondé par Daniel J. Bernstein et Tanja Lange.

Recommandations

Il est important de bien garder en tête que la technologie quantique n’est plus un rêve à l’heure actuelle. De grandes entreprises et puissances mondiales travaillent d’arrache-pied pour être les premiers à obtenir des résultats probants sur les calculs quantiques, mais aussi (et surtout) sur les attaques quantiques. Le premier qui saura réellement casser RSA-1024 aura acquis un pouvoir considérable dans le domaine de la sécurité informatique moderne.

Considérant donc ces faits comme inévitables, voici quelques recommandations sur comment se protéger au mieux des attaques quantiques.

1) La cryptographie asymétrique doit être post-quantique

Il faut commencer à migrer vers des bibliothèques qui implémentent des méthodes de cryptographie post-quantique. C’est le cas de la bibliothèque C open-source liboqs d’Open Quantum Safe.

2) La cryptographie symétrique doit être plus looooooooongue

Une façon simple et efficace de se protéger de l’algorithme de Grover est d’utiliser des clés cryptographiques très longues.

3) L’utilisation de hash-based crypto doit être réfléchie

Tout d’abord, en cas d’utilisation du schéma de Lamport ou du schéma de Merkle, les clés utilisées ne doivent servir qu’une et une seule fois, sinon il sera plus facile à un attaquant de retrouver les clés et de forger de nouvelles signatures. Aussi, comme ces méthodes sont basées sur des fonctions de hachage, la longueur des clés doit être suffisante, comme pour du chiffrement symétrique. Veillez à doubler la taille des clés pour être résistant aux attaques quantiques.

4) code-BASED CRYPTO est une méthode très lourde

L’utilisation de telles méthodes de chiffrement doit être bien considérée avant toute mise en place car la taille des clés publiques est très grande (> 9 Mbits), pouvant affaiblir fortement les performances de certains systèmes.

5) Lattice-based crypto n’est pas assez mature

En effet malgré leur côté très prometteur, ces méthodes sont trop récentes dans le domaine post-quantique, et il existe peu d’études démontrant leur fiabilité et résistance aux attaques quantiques. Il serait plus judicieux d’attendre quelques années avant de faire dépendre la sécurité de tout un système informatique uniquement sur ce type de cryptographie.

En complément

Pour une vision un peu plus large sur la technologie quantique, son fonctionnement, son utilisation pour améliorer la cryptographie actuelle, mais aussi les attaques quantiques et les solutions à ces attaques, le lecteur intéressé peut consulter les slides suivants.