Aanleiding van deze blog is een mail die ik ontving betreffende de moeilijkheid in analytics om causaliteit, en niet louter correlatie, tussen twee fenomenen vast te stellen.
De suggestie dat dit met klassieke statistiek ook niet zou kunnen, en er dus eigenlijk geen probleem is, is betwistbaar. Wél staat vast dat causaliteit vaak een moeilijke kwestie is. Waar gaat het precies over?
Correlatie en causaliteit
Een positieve correlatie tussen twee grootheden (variabelen) X en Y betekent dat wanneer de ene grote (resp. kleine) waarden aanneemt, de andere de neiging heeft dat ook te doen. Een negatieve correlatie betekent dat wanneer de ene grote (resp. kleine) waarden aanneemt, de andere de neiging heeft het tegengestelde te doen.
In onderstaande figuur werden data gesimuleerd volgens een tweedimensionele normale verdeling met een correlatiecoëfficiënt van 0.9 (links) en -0.3 (rechts). Algemeen kan men zeggen dat hoe sterker de correlatie is, hoe duidelijker de bovengenoemde relatie en hoe meer informatie je hebt over de grootte van de ene variabele als je de andere variabele kent.
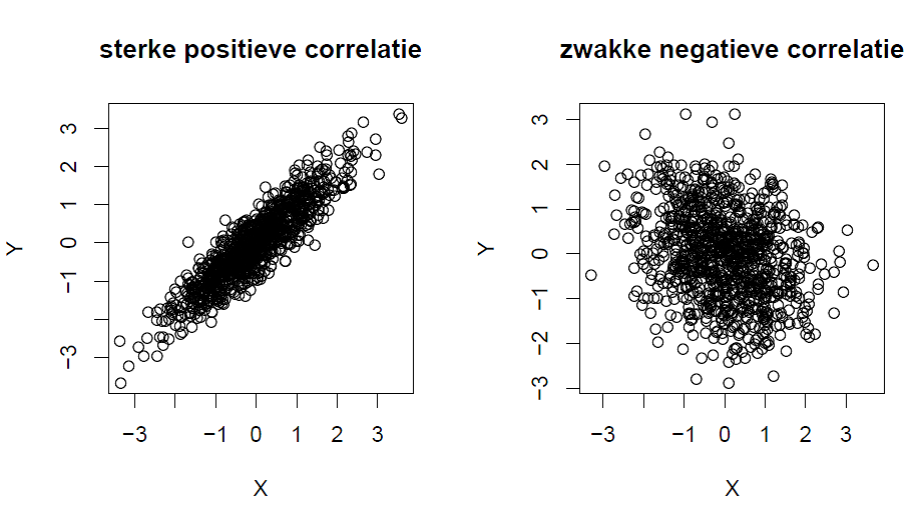
(.pdf generated with R-software)
Causaliteit (oorzakelijkheid) is een sterker begrip, dat weergeeft dat een fenomeen X de oorzaak is van een fenomeen Y. Bijgevolg zal het zich voordoen van fenomeen X het zich voordoen van fenomeen Y beïnvloeden en aldus kan men verwachten dat er een correlatie optreedt tussen X en Y. Causaliteit is sterker omdat je aangeeft dat er een soort van mechanisme is en bovendien heb je daar niet de symmetrie tussen X en Y die je bij een correlatie wél hebt. De gevolgen zijn ook veel zwaarder. Zo men bijvoorbeeld besluit dat de incidentie van longkanker het gevolg is van roken dringen maatregelen zich op om de volksgezondheid te vrijwaren. Vaak is een causaliteitsbesluit echter controversieel en moeilijk te bewijzen.
De bloemetjes en de bijtjes

(public domain picture at www.lifeofpix.com)
Een eenvoudig en ludiek voorbeeld gaat over volgende twee fenomenen:
X: het aantal ooievaarsnesten in een dorp;
Y: het aantal nieuwgeboren baby’s in dat dorp.
In dorpen in de Elzas is begin de 20ste eeuw een correlatie vastgesteld tussen beide fenomenen, wat zou kunnen doen geloven dat de ooievaars effectief tussenkomen in het afleveren van de baby’s. De statisticus George Udny Yule gebruikt dit voorbeeld om aan te tonen dat de correlatie die gezien wordt tussen X en Y geen bewijs is van causaliteit. Uiteraard kennen we de echte causaliteitsverklaring achter de variabele Y, maar het is zeker interessant om even stil te staan bij de vraag waarom deze correlatie bestaat.
Namelijk, er is sprake van een tussenliggende variabele, zeg,
Z: de grootte van het dorp,
die beide X en Y positief beïnvloedt. Inderdaad, een groter dorp biedt meer schoorstenen en torens en heeft tegelijk uiteraard ook een grotere bevolking en dus een groter absoluut geboortecijfer.
Yule gebruikt dit voorbeeld om de lezer uit te leggen wat een confounder is: een externe variabele die met beide variabelen in kwestie gecorreleerd is. Het is geen toeval dat dit voorbeeld opduikt in een boek over statistiek, vanuit de toepassingen waarrond de statistiek zich heeft ontwikkeld is er altijd aandacht geweest voor het causaliteitsvraagstuk, ook al is dit soms erg moeilijk.
Een medicijn gebaseerd op correlatie of causaliteit ?
In het medisch onderzoek bijvoorbeeld staat de causaliteitsvraag vaak centraal. Immers, vooraleer men besluit een nieuw geneesmiddel als veilig en werkzaam te beschouwen voert men studies om zo goed mogelijk zicht te krijgen op de biologische en biochemische werking van een nieuwe molecule, en om er zich van te verzekeren dat de gunstige werking toe te schrijven is aan de therapie en niet aan andere factoren zoals verschillen tussen patiënten (geslacht, leeftijd, genetisch profiel etc). Eén van de mogelijkheden om confounders uit te schakelen is het opzetten van een experiment dat er rekening mee houdt, bijvoorbeeld door het selecteren van homogene groepen van proefpersonen.
Als de gezondheid op het spel staat zijn weinig mensen bereid roekeloze risico’s te nemen, en voor de grote farmaconcerns is de geschiktheid van een nieuw medicijn niet zo maar een vraag maar eerder een million (of billion) dollar question.
Correlaties in analytics
In wezen lijkt het doel van analytics en statistiek volledig hetzelfde, namelijk informatie halen en conclusies trekken uit gegevens. Gebruikers van beide methoden hebben overigens ook gemeen dat men vaak (te) hoge verwachtingen heeft over wat men redelijkerwijze uit de gegeven data kan besluiten. Toch is de werkwijze radicaal anders. Waar men in de statistiek gericht en gepland te werk gaat (of hoort dat te doen), probeert men in analytics vooral kracht te halen uit het combineren van grote hoeveelheden data en het doorrekenen van grote aantallen algoritmes. Waar bij statistische studies de methodologie centraal staat, lijkt het bij analytics vooral over het snelle resultaat te gaan, zonder veel oog voor methodologische problemen en valkuilen, zoals bijvoorbeeld data-quality problemen.
Het opgeven van het causaliteitsvraagstuk is dus in zekere zin inherent aan de manier van werken in analytics, en kan gezien worden als de prijs die betaald moet worden voor snelle en automatische resultaten.
Zin en onzin van correlaties
Websites met bloemlezingen van bedenkelijke, grappige of bizarre correlaties, vaak tussen tijdreeksen, zijn een groot succes op internet. Dit betekent niet dat correlaties per definitie zinloos zijn. Het hangt alleen af van de beoogde toepassing en vakgebied. Zo bijvoorbeeld zal het een marketeer worst wezen waarom precies doelgroep X interesse heeft in product Y. Het feit dat het zo is en dat hij of zij dit als eerste ontdekt werd kan al ruim voldoende zijn om de verkoopscijfers op te krikken.
Als het misgaat
Is uiteindelijk natuurlijk de gebruiker verantwoordelijk. De analytics tool, ook al wordt die voorgesteld als een soort elektronische Einstein, is niets meer dan een machine en het is de gebruiker die beslist welke gevolgen te geven aan één of andere uitkomst. Misschien is dat het openen van een extra verkooppunt om de doelgroep X te bedienen, maar misschien is dat de beslissing om één en ander verder te onderzoeken, op basis van een meer beproefde methodologie indien grote risico’s niet uit te sluiten zijn.
Tot besluit: analytics en statistiek
Als besluit moet zeker opgemerkt worden dat statistiek als vakgebied zich dank zij de computer heel snel heeft kunnen ontwikkelen. Vele statistische procedures steunen immers op rekenintensieve (iteratieve) algoritmen die met de hand praktisch onuitvoerbaar zouden zijn, om nog maar te zwijgen over de faciliteiten die de computer biedt om data te beheren. Evenzeer lijkt op te gaan dat de analytics approach kan vooruitgaan door de overwegingen van statistiek mee te nemen. De prijs die betaald moet worden is mogelijk een langere doorlooptijd en het opgeven van een volledig automatische verwerking maar voor sommige toepassingen is dat ongetwijfeld een goede, zelfs noodzakelijke, investering.

De causaliteit-uitdaging voor analytics en statistiek worden vandaag aangepakt met “gezond verstand”. Dat heeft ook zijn prijs, of zeg maar risico.
Er is bijvoorbeeld een correlatie tussen (a) wat langer slapen en (b) extra haasten om mijn trein te halen. Mijn gezond verstand zegt dat (a) de oorzaak is van (b) en niet omgekeerd. Maar zelfs gezond verstand kan zich vergissen. En dat is een extra prijs die we betalen. Wist je bijvoorbeeld dat de gepensioneerden bij de meest tevreden klanten van de bank horen? Dat is niet omdat zij beter advies krijgen, maar wel omdat zij (50 jaar geleden) minder hoger onderwijs hebben gevolgd, minder complexe diensten afnemen… Met analytics heb je misschien een betere ondersteuning van het gezond verstand.